排序算法用于按特定顺序排列数组/列表的元素。例如,
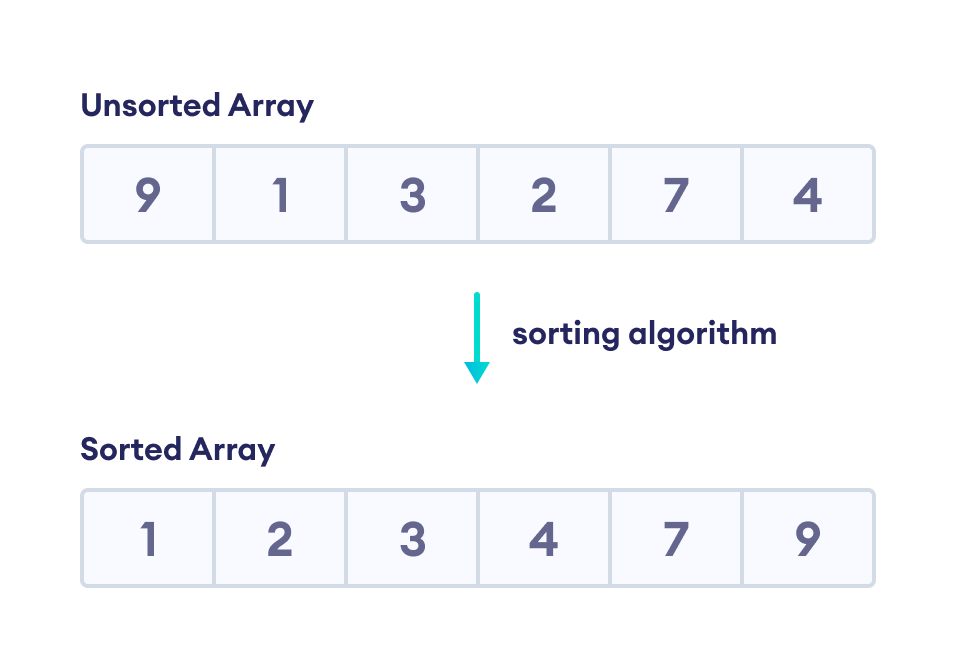
在这里,我们按升序对数组进行排序。
有各种排序算法可用于完成此操作。并且,我们可以根据需要使用任何算法。
不同的排序算法
排序算法的复杂度
任何排序算法的效率都由算法的时间复杂度和空间复杂度决定。
1. 时间复杂度:时间复杂度是指算法相对于输入大小完成其执行所需的时间。它可以表示为不同的形式
2. 空间复杂度:空间复杂度是指算法在完全执行期间使用的总内存量。它包括辅助内存和输入。
辅助内存是算法除输入数据外占用的附加空间。通常,在计算算法的空间复杂度时会考虑辅助内存。
让我们看一下不同排序算法的复杂度分析。
| 排序算法 | 时间复杂度 - 最佳 | 时间复杂度 - 最差 | 时间复杂度 - 平均 | 空间复杂度 |
|---|---|---|---|---|
| 冒泡排序 | n | n2 | n2 | 1 |
| 选择排序 | n2 | n2 | n2 | 1 |
| 插入排序 | n | n2 | n2 | 1 |
| 归并排序 | nlog n | nlog n | nlog n | n |
| 快速排序 | nlog n | n2 | nlog n | log n |
| 计数排序 | n+k | n+k | n+k | max |
| 基数排序 | n+k | n+k | n+k | max |
| 桶排序 | n+k | n2 | n | n+k |
| 堆排序 | nlog n | nlog n | nlog n | 1 |
| 希尔排序 | nlog n | n2 | nlog n | 1 |
排序算法的稳定性
如果两个或多个具有相同值的项在排序后保持相同的相对位置,则认为该排序算法是稳定的。
例如,在下图中,有两个值均为 3 的项。不稳定的排序算法允许两种可能性,即 3 的两个位置可能被保留,也可能不被保留。
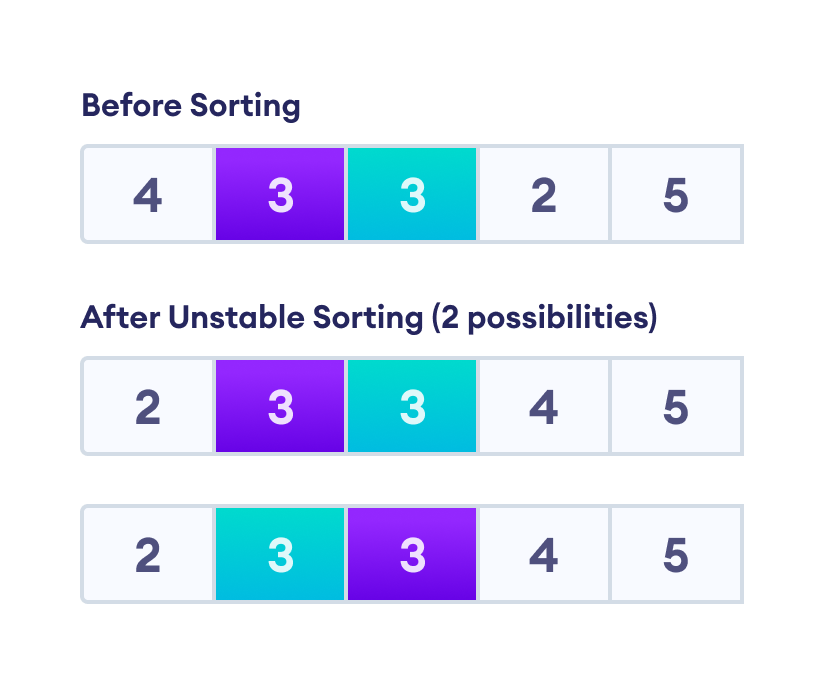
但是,在稳定的排序算法之后,总有一种可能性,即位置会像原始数组一样被保留。
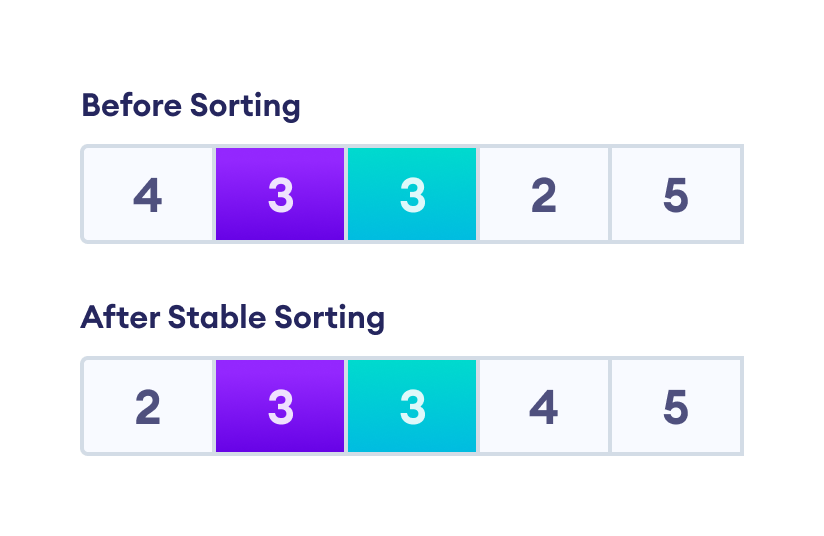
下面是一个表格,显示了不同排序算法的稳定性。
| 排序算法 | 稳定性 |
|---|---|
| 冒泡排序 | 是 |
| 选择排序 | 否 |
| 插入排序 | 是 |
| 归并排序 | 是 |
| 快速排序 | 否 |
| 计数排序 | 是 |
| 基数排序 | 是 |
| 桶排序 | 是 |
| 堆排序 | 否 |
| 希尔排序 | 否 |
