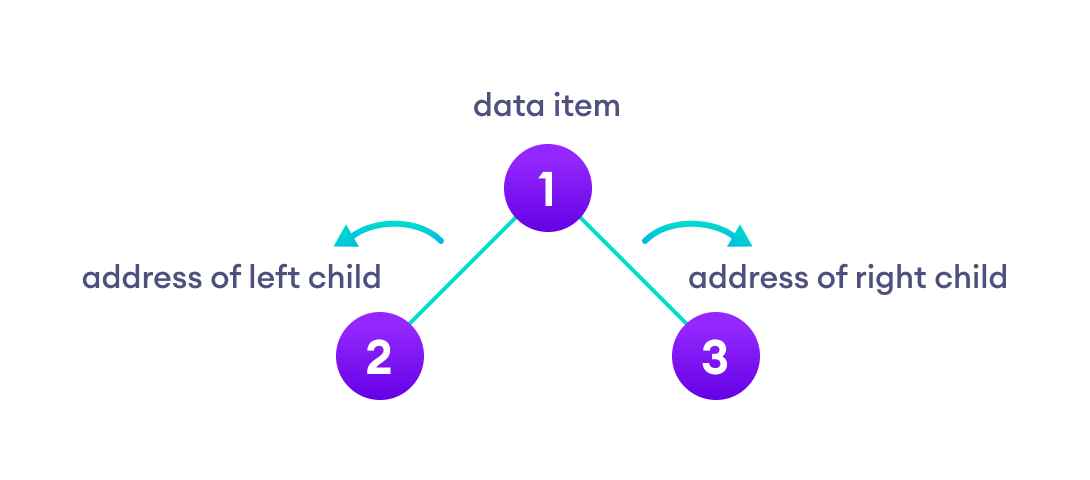
二叉树是一种树形数据结构,其中每个父节点最多有两个子节点。二叉树的每个节点包含三项:
-
数据项
-
左子节点的地址
-
右子节点的地址
二叉树的类型
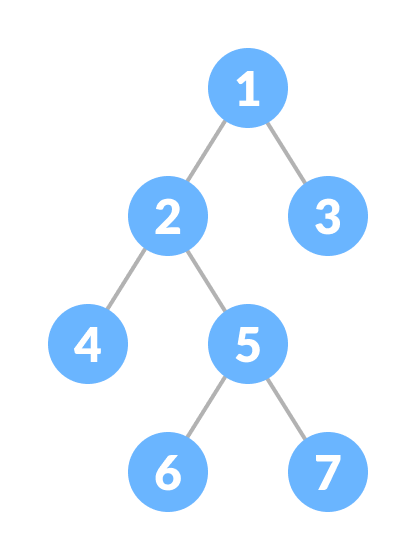
1. 满二叉树
满二叉树是一种特殊的二叉树,其中每个父节点/内部节点要么有两个子节点,要么没有子节点。
要了解更多信息,请访问 满二叉树。
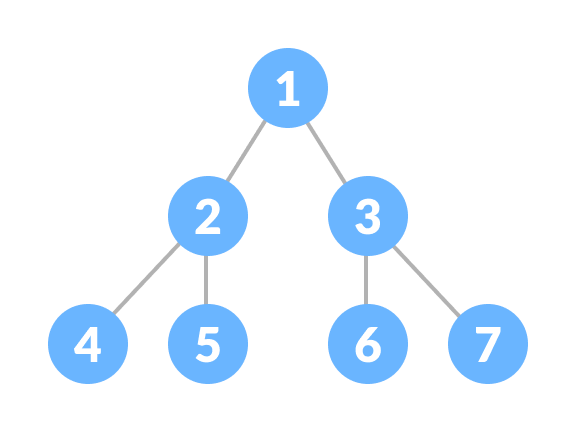
2. 完全二叉树
完全二叉树是一种二叉树,其中每个内部节点恰好有两个子节点,并且所有叶节点都处于同一层。
要了解更多信息,请访问 完全二叉树。
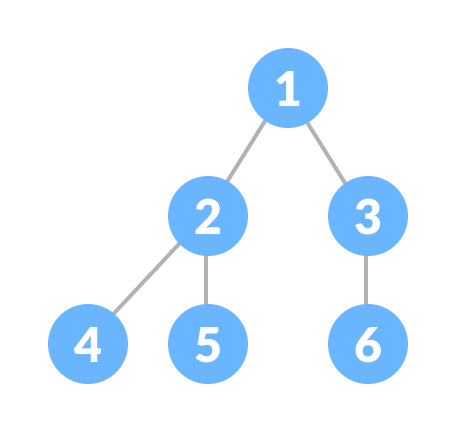
3. 完满二叉树
完满二叉树与满二叉树相似,但有两个主要区别:
- 每一层都必须完全填满
- 所有叶子节点必须靠左排列。
- 最后一个叶子节点可能没有右兄弟,也就是说,完满二叉树不一定是满二叉树。
要了解更多信息,请访问 完满二叉树。
4. 退化二叉树或病态二叉树
退化二叉树或病态二叉树是指只有一个子节点(左或右)的树。
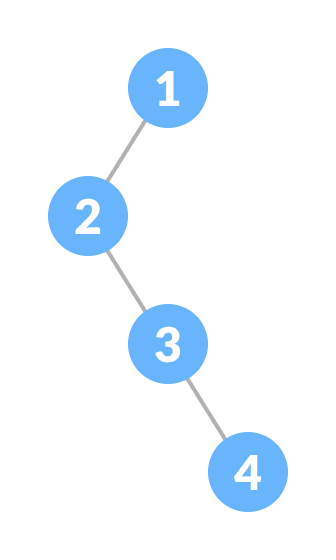
5. 倾斜二叉树
倾斜二叉树是一种病态/退化二叉树,其中树主要由左节点或右节点构成。因此,倾斜二叉树有两种类型:**左倾斜二叉树**和**右倾斜二叉树**。
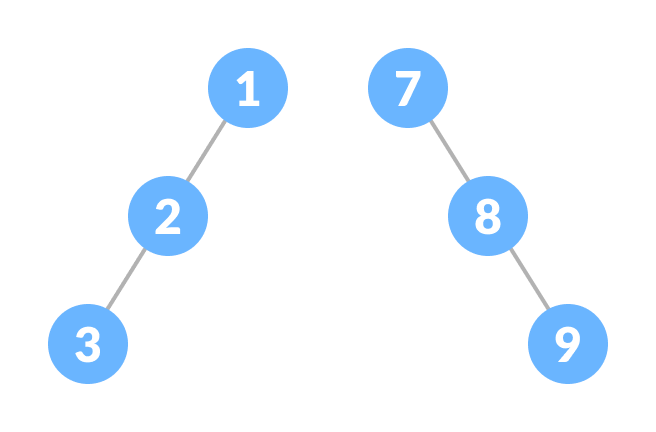
6. 平衡二叉树
这是一种二叉树,其中每个节点的左子树和右子树的高度差为0或1。
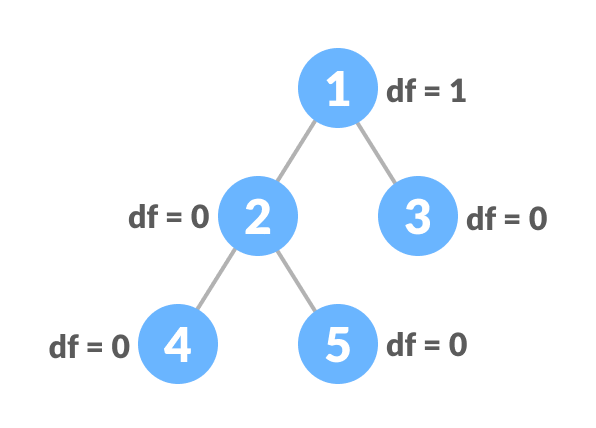
要了解更多信息,请访问 平衡二叉树。
二叉树表示
二叉树的节点由一个结构表示,该结构包含数据部分和指向同类型其他结构的两个指针。
struct node
{
int data;
struct node *left;
struct node *right;
};
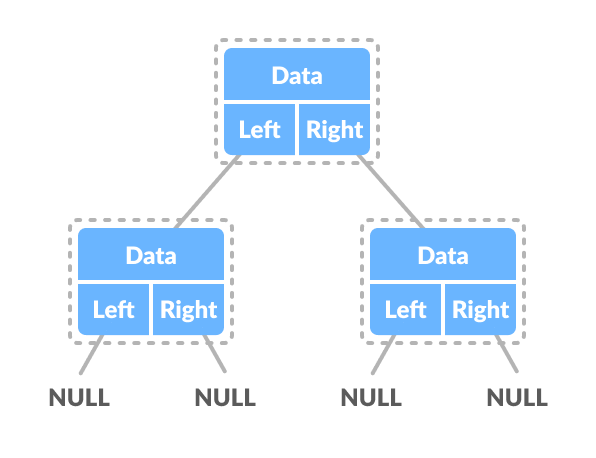
Python、Java 和 C/C++ 示例
# Binary Tree in Python
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
# Traverse preorder
def traversePreOrder(self):
print(self.val, end=' ')
if self.left:
self.left.traversePreOrder()
if self.right:
self.right.traversePreOrder()
# Traverse inorder
def traverseInOrder(self):
if self.left:
self.left.traverseInOrder()
print(self.val, end=' ')
if self.right:
self.right.traverseInOrder()
# Traverse postorder
def traversePostOrder(self):
if self.left:
self.left.traversePostOrder()
if self.right:
self.right.traversePostOrder()
print(self.val, end=' ')
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
print("Pre order Traversal: ", end="")
root.traversePreOrder()
print("\nIn order Traversal: ", end="")
root.traverseInOrder()
print("\nPost order Traversal: ", end="")
root.traversePostOrder()// Binary Tree in Java
// Node creation
class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree(int key) {
root = new Node(key);
}
BinaryTree() {
root = null;
}
// Traverse Inorder
public void traverseInOrder(Node node) {
if (node != null) {
traverseInOrder(node.left);
System.out.print(" " + node.key);
traverseInOrder(node.right);
}
}
// Traverse Postorder
public void traversePostOrder(Node node) {
if (node != null) {
traversePostOrder(node.left);
traversePostOrder(node.right);
System.out.print(" " + node.key);
}
}
// Traverse Preorder
public void traversePreOrder(Node node) {
if (node != null) {
System.out.print(" " + node.key);
traversePreOrder(node.left);
traversePreOrder(node.right);
}
}
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
System.out.print("Pre order Traversal: ");
tree.traversePreOrder(tree.root);
System.out.print("\nIn order Traversal: ");
tree.traverseInOrder(tree.root);
System.out.print("\nPost order Traversal: ");
tree.traversePostOrder(tree.root);
}
}// Tree traversal in C
#include <stdio.h>
#include <stdlib.h>
struct node {
int item;
struct node* left;
struct node* right;
};
// Inorder traversal
void inorderTraversal(struct node* root) {
if (root == NULL) return;
inorderTraversal(root->left);
printf("%d ->", root->item);
inorderTraversal(root->right);
}
// Preorder traversal
void preorderTraversal(struct node* root) {
if (root == NULL) return;
printf("%d ->", root->item);
preorderTraversal(root->left);
preorderTraversal(root->right);
}
// Postorder traversal
void postorderTraversal(struct node* root) {
if (root == NULL) return;
postorderTraversal(root->left);
postorderTraversal(root->right);
printf("%d ->", root->item);
}
// Create a new Node
struct node* createNode(value) {
struct node* newNode = malloc(sizeof(struct node));
newNode->item = value;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// Insert on the left of the node
struct node* insertLeft(struct node* root, int value) {
root->left = createNode(value);
return root->left;
}
// Insert on the right of the node
struct node* insertRight(struct node* root, int value) {
root->right = createNode(value);
return root->right;
}
int main() {
struct node* root = createNode(1);
insertLeft(root, 2);
insertRight(root, 3);
insertLeft(root->left, 4);
printf("Inorder traversal \n");
inorderTraversal(root);
printf("\nPreorder traversal \n");
preorderTraversal(root);
printf("\nPostorder traversal \n");
postorderTraversal(root);
}// Binary Tree in C++
#include <stdlib.h>
#include <iostream>
using namespace std;
struct node {
int data;
struct node *left;
struct node *right;
};
// New node creation
struct node *newNode(int data) {
struct node *node = (struct node *)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
// Traverse Preorder
void traversePreOrder(struct node *temp) {
if (temp != NULL) {
cout << " " << temp->data;
traversePreOrder(temp->left);
traversePreOrder(temp->right);
}
}
// Traverse Inorder
void traverseInOrder(struct node *temp) {
if (temp != NULL) {
traverseInOrder(temp->left);
cout << " " << temp->data;
traverseInOrder(temp->right);
}
}
// Traverse Postorder
void traversePostOrder(struct node *temp) {
if (temp != NULL) {
traversePostOrder(temp->left);
traversePostOrder(temp->right);
cout << " " << temp->data;
}
}
int main() {
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
cout << "preorder traversal: ";
traversePreOrder(root);
cout << "\nInorder traversal: ";
traverseInOrder(root);
cout << "\nPostorder traversal: ";
traversePostOrder(root);
}二叉树的应用
- 为了方便快速访问数据
- 在路由器算法中
- 用于实现 堆数据结构
- 语法树
