快速排序算法

快速排序是一种基于分治法的排序算法，其中

通过选择一个枢轴元素（从数组中选取的元素）将数组划分为子数组。

在划分数组时，枢轴元素应放置在使得小于枢轴的元素位于枢轴的左侧，大于枢轴的元素位于枢轴的右侧的位置。
左右子数组也使用相同的方法进行划分。此过程一直持续到每个子数组只包含一个元素。
此时，元素已排序。最后，将元素组合起来形成一个已排序的数组。

快速排序算法的工作原理

1. 选择枢轴元素

快速排序有不同的变体，其中枢轴元素从不同的位置选择。在这里，我们将选择数组的最后一个元素作为枢轴元素。

2. 重排数组

现在，数组的元素被重新排列，以便小于枢轴的元素放在左边，大于枢轴的元素放在右边。

我们这样重排数组

将一个指针固定在枢轴元素上。将枢轴元素与从第一个索引开始的元素进行比较。

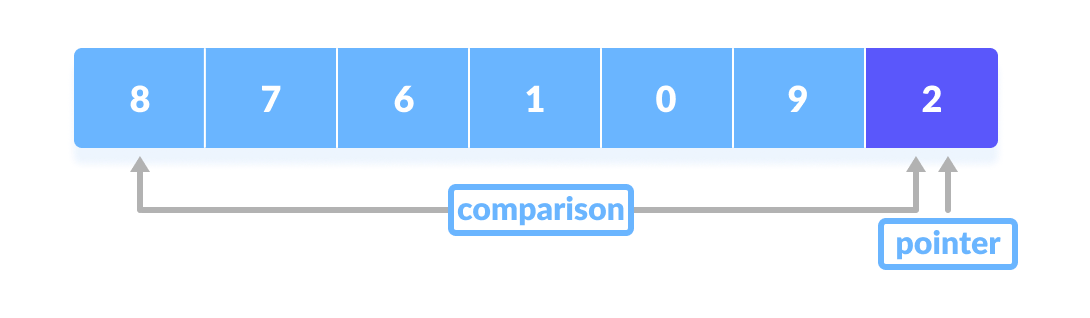
将枢轴元素与从第一个索引开始的元素进行比较
如果元素大于枢轴元素，则为该元素设置第二个指针。

如果元素大于枢轴元素，则为该元素设置第二个指针。
现在，将枢轴与其他元素进行比较。如果遇到小于枢轴元素的元素，则将较小的元素与之前找到的较大元素进行交换。

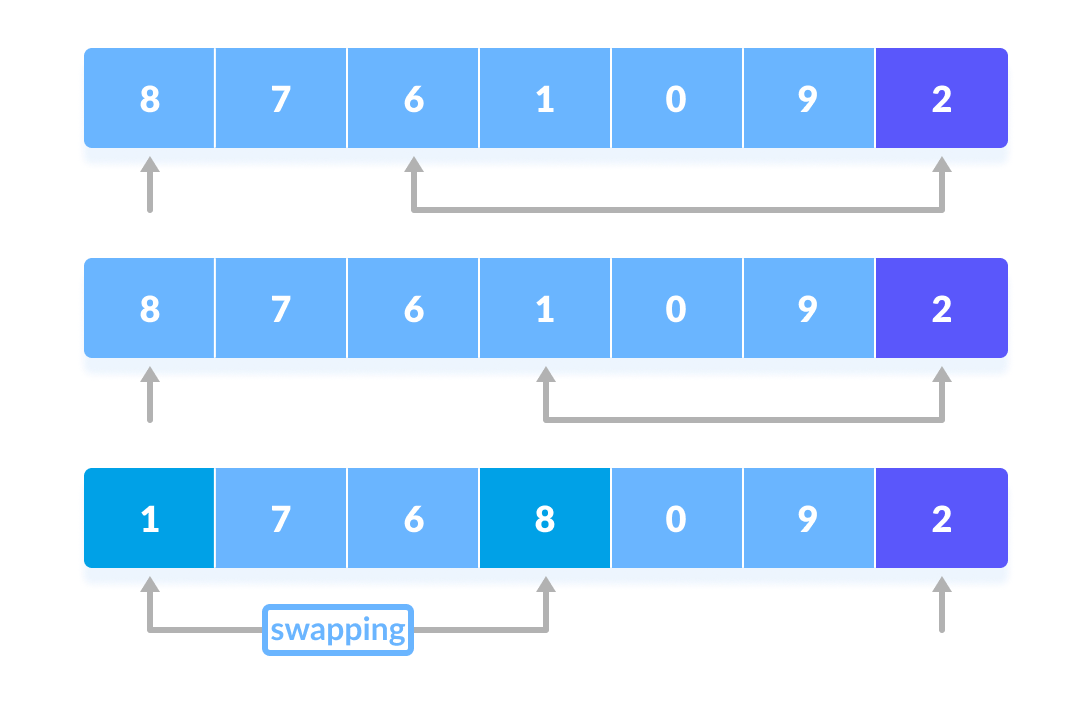
枢轴与其他元素进行比较。
再次，重复此过程，将下一个较大的元素设置为第二个指针。然后，将其与另一个较小的元素交换。

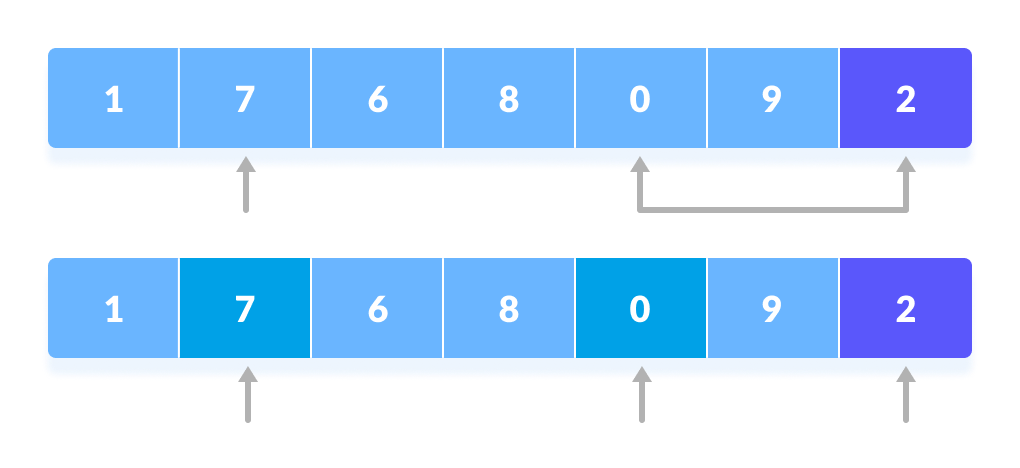
重复此过程，将下一个较大的元素设置为第二个指针。
过程一直持续到到达倒数第二个元素。

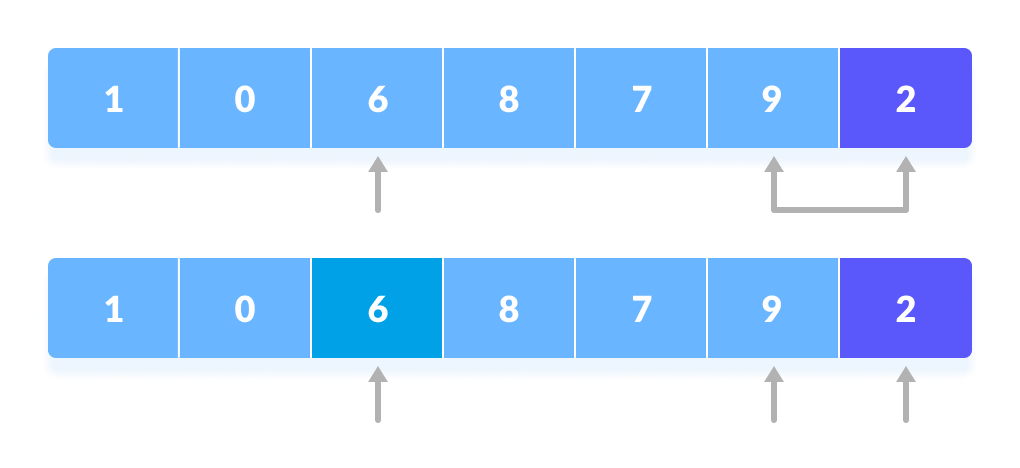
过程一直持续到到达倒数第二个元素。
最后，将枢轴元素与第二个指针交换。

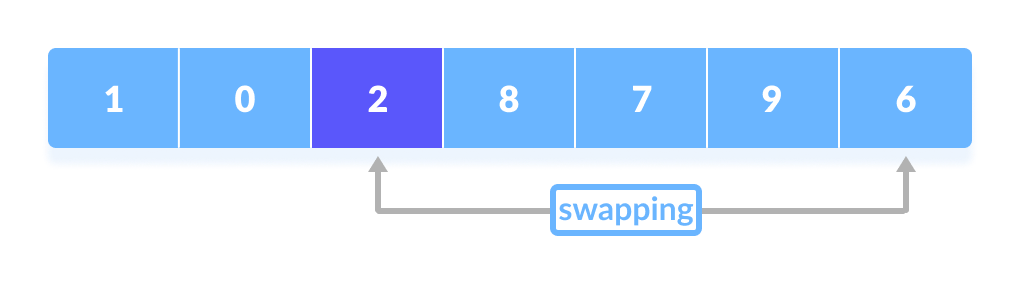
最后，将枢轴元素与第二个指针交换。

3. 划分子数组

再次分别选择左右子部分的枢轴元素。然后，重复步骤 2。

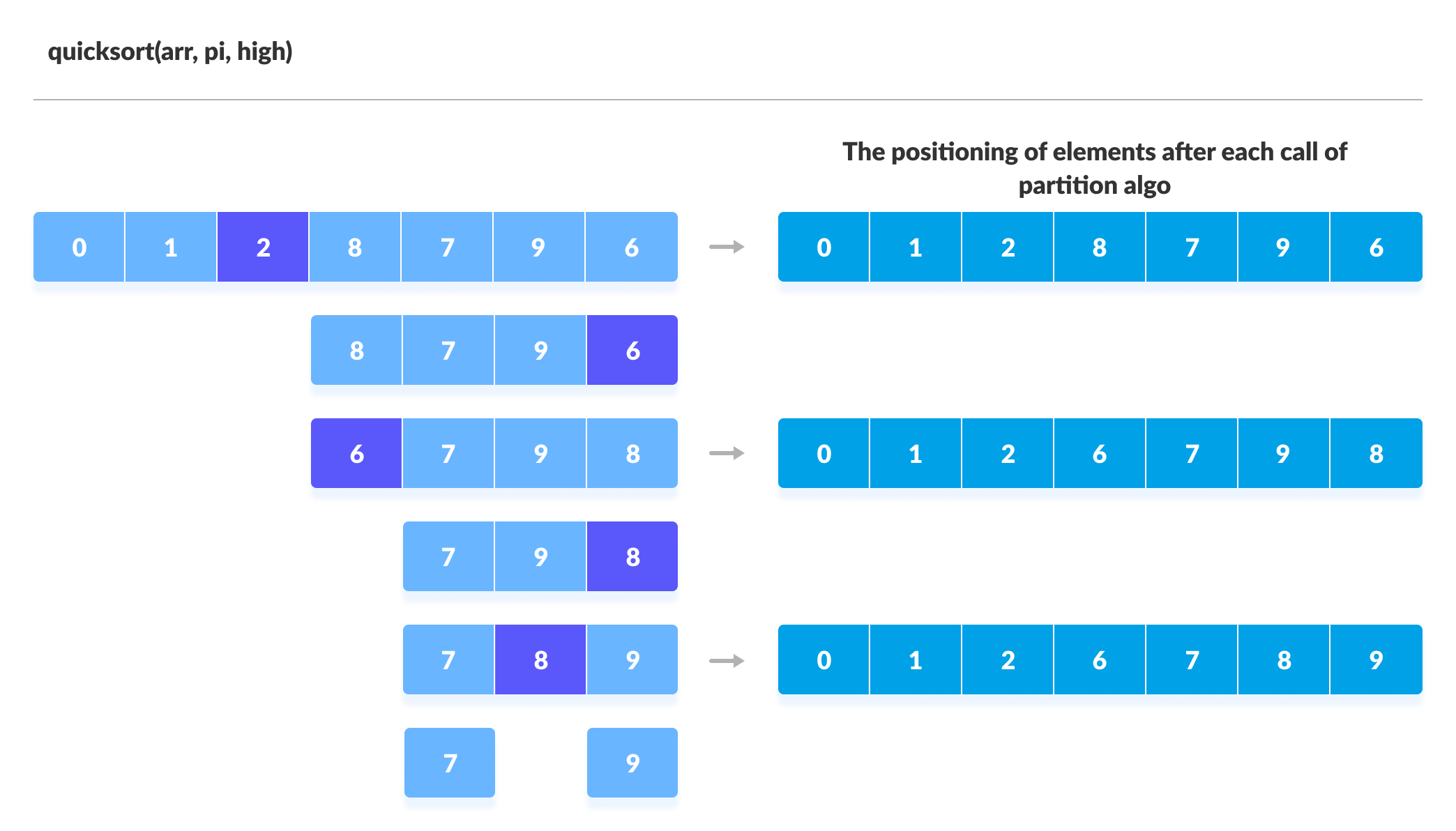
子数组被划分，直到每个子数组由单个元素组成。此时，数组已排序。

快速排序算法


quickSort(array, leftmostIndex, rightmostIndex)
  if (leftmostIndex < rightmostIndex)
    pivotIndex <- partition(array,leftmostIndex, rightmostIndex)
    quickSort(array, leftmostIndex, pivotIndex - 1)
    quickSort(array, pivotIndex, rightmostIndex)

partition(array, leftmostIndex, rightmostIndex)
  set rightmostIndex as pivotIndex
  storeIndex <- leftmostIndex - 1
  for i <- leftmostIndex + 1 to rightmostIndex
  if element[i] < pivotElement
    swap element[i] and element[storeIndex]
    storeIndex++
  swap pivotElement and element[storeIndex+1]
return storeIndex + 1

快速排序算法的直观图

您可以通过下面的图示来理解快速排序算法的工作原理。

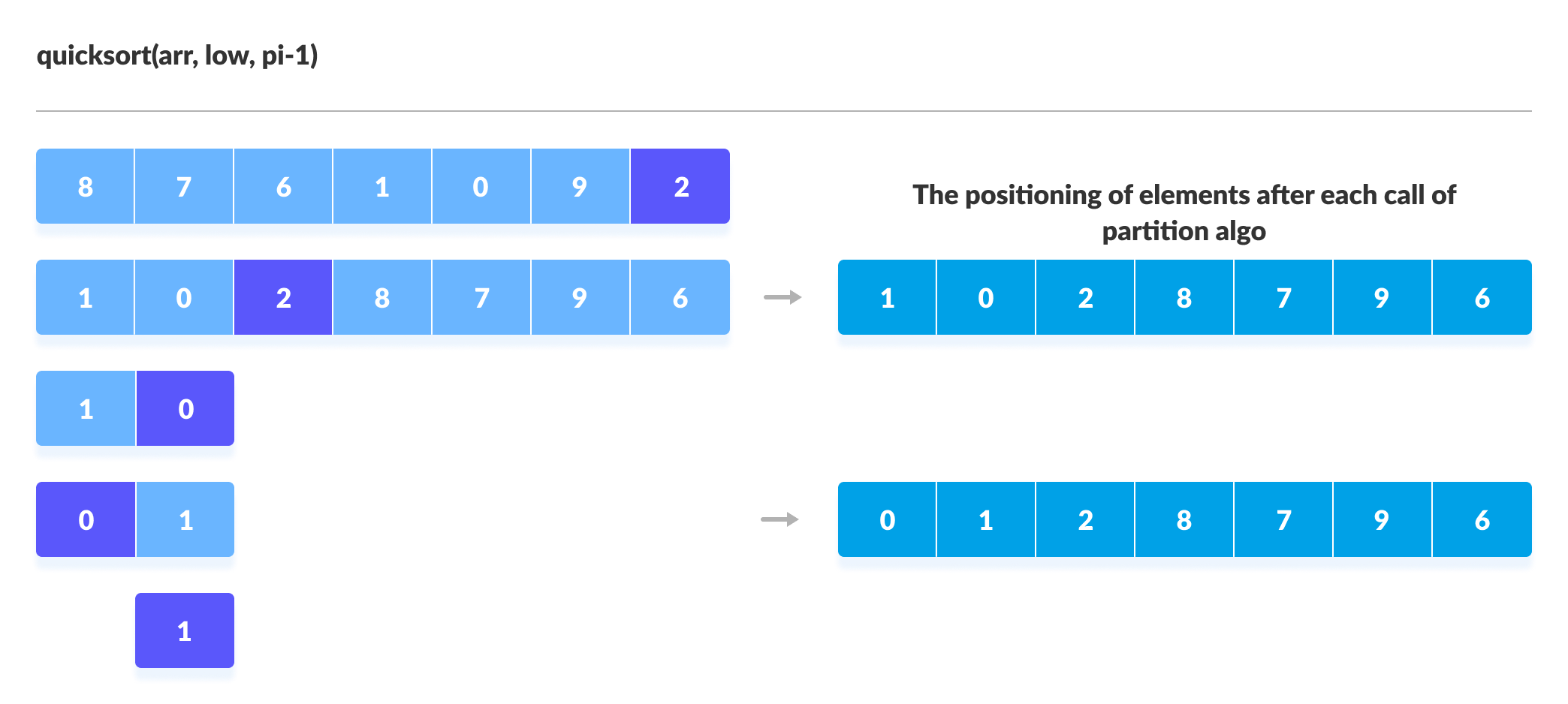
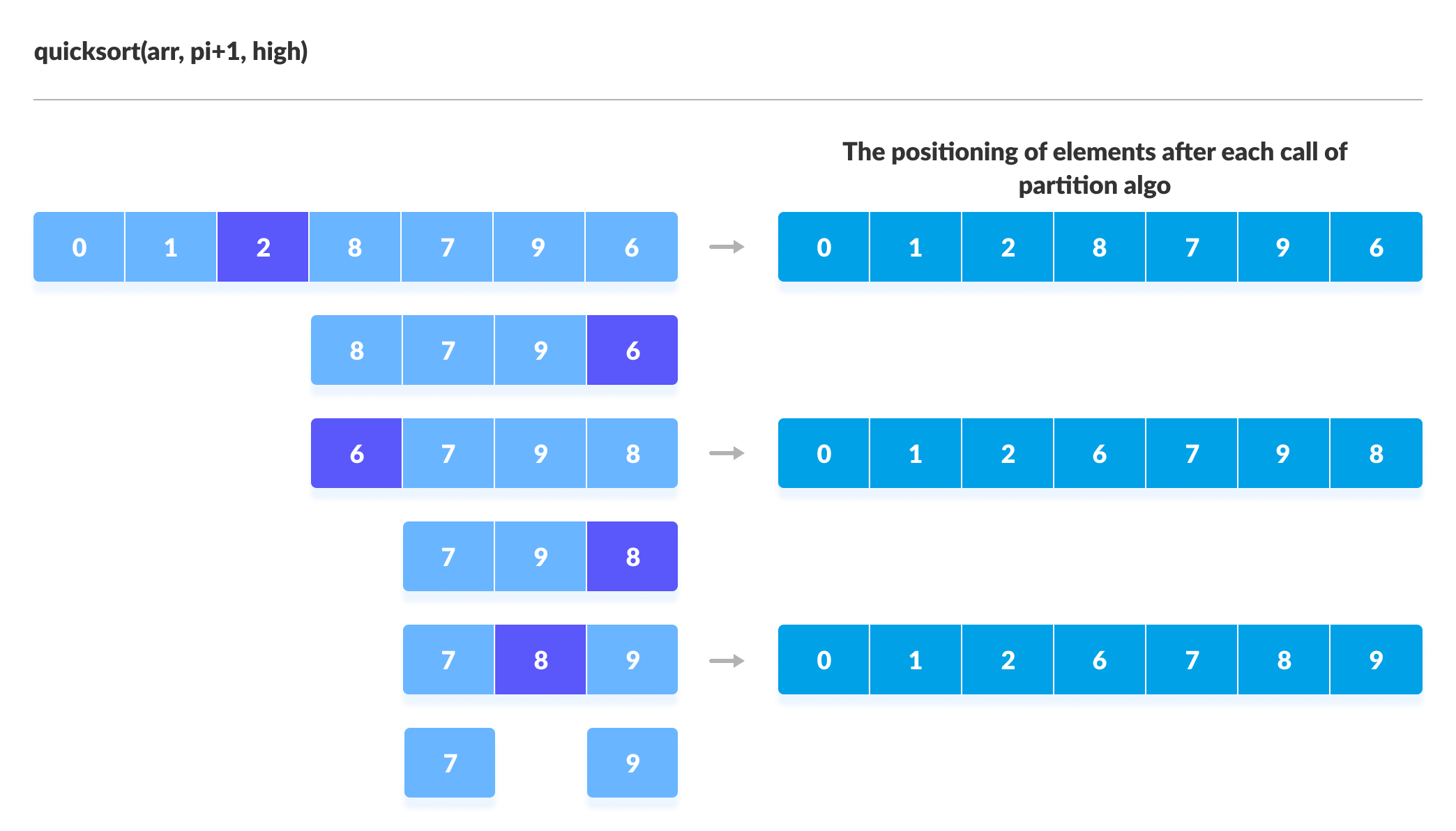
Python、Java 和 C/C++ 中的快速排序代码

Python

Java

C++

# Quick sort in Python

# function to find the partition position
def partition(array, low, high):

  # choose the rightmost element as pivot
  pivot = array[high]

  # pointer for greater element
  i = low - 1

  # traverse through all elements
  # compare each element with pivot
  for j in range(low, high):
    if array[j] <= pivot:
      # if element smaller than pivot is found
      # swap it with the greater element pointed by i
      i = i + 1

      # swapping element at i with element at j
      (array[i], array[j]) = (array[j], array[i])

  # swap the pivot element with the greater element specified by i
  (array[i + 1], array[high]) = (array[high], array[i + 1])

  # return the position from where partition is done
  return i + 1

# function to perform quicksort
def quickSort(array, low, high):
  if low < high:

    # find pivot element such that
    # element smaller than pivot are on the left
    # element greater than pivot are on the right
    pi = partition(array, low, high)

    # recursive call on the left of pivot
    quickSort(array, low, pi - 1)

    # recursive call on the right of pivot
    quickSort(array, pi + 1, high)


data = [8, 7, 2, 1, 0, 9, 6]
print("Unsorted Array")
print(data)

size = len(data)

quickSort(data, 0, size - 1)

print('Sorted Array in Ascending Order:')
print(data)

// Quick sort in Java

import java.util.Arrays;

class Quicksort {

  // method to find the partition position
  static int partition(int array[], int low, int high) {
    
    // choose the rightmost element as pivot
    int pivot = array[high];
    
    // pointer for greater element
    int i = (low - 1);

    // traverse through all elements
    // compare each element with pivot
    for (int j = low; j < high; j++) {
      if (array[j] <= pivot) {

        // if element smaller than pivot is found
        // swap it with the greatr element pointed by i
        i++;

        // swapping element at i with element at j
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
      }

    }

    // swapt the pivot element with the greater element specified by i
    int temp = array[i + 1];
    array[i + 1] = array[high];
    array[high] = temp;

    // return the position from where partition is done
    return (i + 1);
  }

  static void quickSort(int array[], int low, int high) {
    if (low < high) {

      // find pivot element such that
      // elements smaller than pivot are on the left
      // elements greater than pivot are on the right
      int pi = partition(array, low, high);
      
      // recursive call on the left of pivot
      quickSort(array, low, pi - 1);

      // recursive call on the right of pivot
      quickSort(array, pi + 1, high);
    }
  }
}

// Main class
class Main {
  public static void main(String args[]) {

    int[] data = { 8, 7, 2, 1, 0, 9, 6 };
    System.out.println("Unsorted Array");
    System.out.println(Arrays.toString(data));

    int size = data.length;

    // call quicksort() on array data
    Quicksort.quickSort(data, 0, size - 1);

    System.out.println("Sorted Array in Ascending Order: ");
    System.out.println(Arrays.toString(data));
  }
}

// Quick sort in C

#include <stdio.h>

// function to swap elements
void swap(int *a, int *b) {
  int t = *a;
  *a = *b;
  *b = t;
}

// function to find the partition position
int partition(int array[], int low, int high) {
  
  // select the rightmost element as pivot
  int pivot = array[high];
  
  // pointer for greater element
  int i = (low - 1);

  // traverse each element of the array
  // compare them with the pivot
  for (int j = low; j < high; j++) {
    if (array[j] <= pivot) {
        
      // if element smaller than pivot is found
      // swap it with the greater element pointed by i
      i++;
      
      // swap element at i with element at j
      swap(&array[i], &array[j]);
    }
  }

  // swap the pivot element with the greater element at i
  swap(&array[i + 1], &array[high]);
  
  // return the partition point
  return (i + 1);
}

void quickSort(int array[], int low, int high) {
  if (low < high) {
    
    // find the pivot element such that
    // elements smaller than pivot are on left of pivot
    // elements greater than pivot are on right of pivot
    int pi = partition(array, low, high);
    
    // recursive call on the left of pivot
    quickSort(array, low, pi - 1);
    
    // recursive call on the right of pivot
    quickSort(array, pi + 1, high);
  }
}

// function to print array elements
void printArray(int array[], int size) {
  for (int i = 0; i < size; ++i) {
    printf("%d  ", array[i]);
  }
  printf("\n");
}

// main function
int main() {
  int data[] = {8, 7, 2, 1, 0, 9, 6};
  
  int n = sizeof(data) / sizeof(data[0]);
  
  printf("Unsorted Array\n");
  printArray(data, n);
  
  // perform quicksort on data
  quickSort(data, 0, n - 1);
  
  printf("Sorted array in ascending order: \n");
  printArray(data, n);
}

// Quick sort in C++

#include <iostream>
using namespace std;

// function to swap elements
void swap(int *a, int *b) {
  int t = *a;
  *a = *b;
  *b = t;
}

// function to print the array
void printArray(int array[], int size) {
  int i;
  for (i = 0; i < size; i++)
    cout << array[i] << " ";
  cout << endl;
}

// function to rearrange array (find the partition point)
int partition(int array[], int low, int high) {
    
  // select the rightmost element as pivot
  int pivot = array[high];
  
  // pointer for greater element
  int i = (low - 1);

  // traverse each element of the array
  // compare them with the pivot
  for (int j = low; j < high; j++) {
    if (array[j] <= pivot) {
        
      // if element smaller than pivot is found
      // swap it with the greater element pointed by i
      i++;
      
      // swap element at i with element at j
      swap(&array[i], &array[j]);
    }
  }
  
  // swap pivot with the greater element at i
  swap(&array[i + 1], &array[high]);
  
  // return the partition point
  return (i + 1);
}

void quickSort(int array[], int low, int high) {
  if (low < high) {
      
    // find the pivot element such that
    // elements smaller than pivot are on left of pivot
    // elements greater than pivot are on righ of pivot
    int pi = partition(array, low, high);

    // recursive call on the left of pivot
    quickSort(array, low, pi - 1);

    // recursive call on the right of pivot
    quickSort(array, pi + 1, high);
  }
}

// Driver code
int main() {
  int data[] = {8, 7, 6, 1, 0, 9, 2};
  int n = sizeof(data) / sizeof(data[0]);
  
  cout << "Unsorted Array: \n";
  printArray(data, n);
  
  // perform quicksort on data
  quickSort(data, 0, n - 1);
  
  cout << "Sorted array in ascending order: \n";
  printArray(data, n);
}

快速排序复杂度

时间复杂度
最佳	O(n*log n)
最坏	O(n²)
平均	O(n*log n)
空间复杂度	O(log n)
稳定性	否

1. 时间复杂度

最坏情况复杂度 [Big-O]: O(n²)
当选择的枢轴元素是最大或最小元素时，就会发生这种情况。

这种情况导致枢轴元素位于已排序数组的极端末端。一个子数组始终为空，另一个子数组包含 n - 1 个元素。因此，快速排序仅在此子数组上调用。

然而，对于分散的枢轴，快速排序算法的性能更好。

最佳情况复杂度 [Big-omega]: O(n*log n)
当枢轴元素始终是中间元素或接近中间元素时，就会发生这种情况。
平均情况复杂度 [Big-theta]: O(n*log n)
当上述情况不发生时，就会发生这种情况。

2. 空间复杂度

快速排序的空间复杂度为 O(log n)。

快速排序的应用

当以下情况时，使用快速排序算法

编程语言适合递归
时间复杂度很重要
空间复杂度很重要

热门教程

热门实例

参考资料

认证课程

成为一名认证的 Python
程序员。

热门教程

参考资料

热门实例

DSA 简介

数据结构 (I)

数据结构 (II)

基于树的 DSA (I)

基于树的 DSA (II)

基于图的 DSA

排序和搜索算法

贪婪算法

动态规划

其他算法

快速排序算法

快速排序算法的工作原理

快速排序算法

快速排序算法的直观图

Python、Java 和 C/C++ 中的快速排序代码

快速排序复杂度

1. 时间复杂度

2. 空间复杂度

快速排序的应用

类似的排序算法

目录

热门教程

热门实例

参考资料

认证课程

成为一名认证的 Python程序员。

热门教程

参考资料

热门实例

DSA 简介

数据结构 (I)

数据结构 (II)

基于树的 DSA (I)

基于树的 DSA (II)

基于图的 DSA

排序和搜索算法

贪婪算法

动态规划

其他算法

DSA 教程

快速排序算法

快速排序算法的工作原理

快速排序算法

快速排序算法的直观图

Python、Java 和 C/C++ 中的快速排序代码

快速排序复杂度

1. 时间复杂度

2. 空间复杂度

快速排序的应用

类似的排序算法

目录

相关教程

成为一名认证的 Python
程序员。