遍历树意味着访问树中的每个节点。例如,您可能想将树中的所有值相加,或者找到最大的值。对于所有这些操作,您都需要访问树的每个节点。
数组、栈、队列和链表等线性数据结构只有一种读取数据的方式。但是,像树这样的分层数据结构可以以不同的方式遍历。
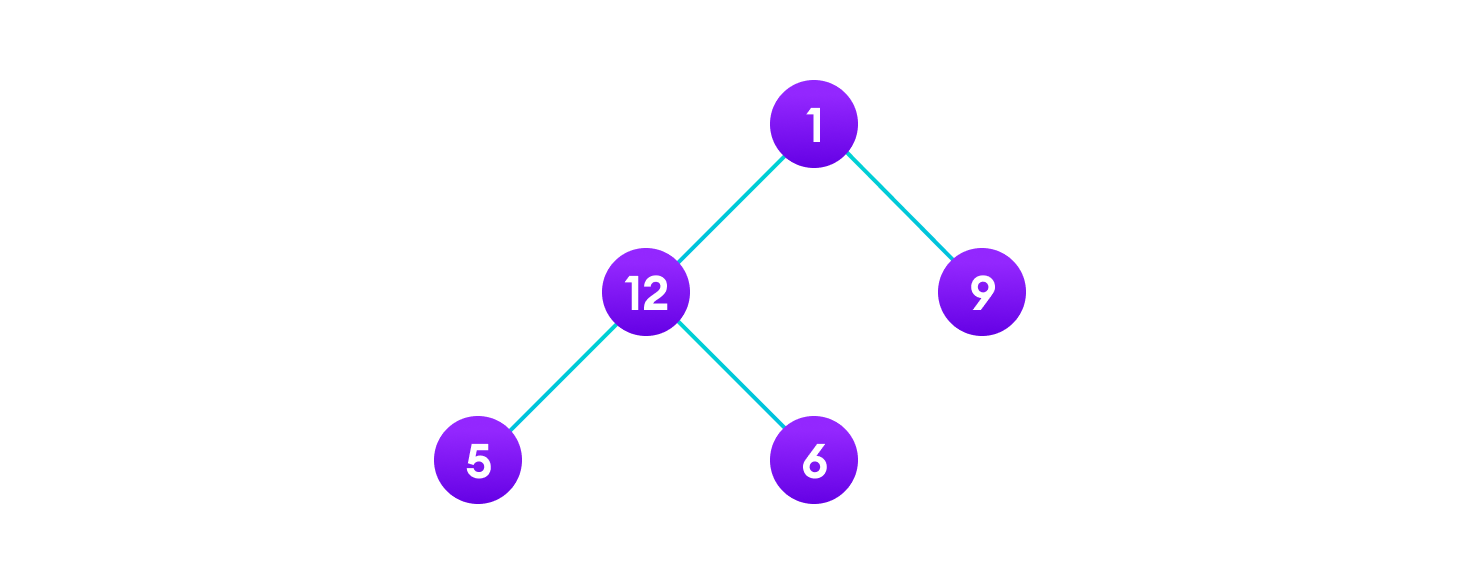
让我们想想如何读取上图中树的元素。
从上到下,从左到右
1 -> 12 -> 5 -> 6 -> 9从下到上,从左到右
5 -> 6 -> 12 -> 9 -> 1虽然这个过程有些简单,但它并不遵循树的层次结构,只遵循节点的深度。
相反,我们使用考虑树的基本结构即的遍历方法。
struct node {
int data;
struct node* left;
struct node* right;
}由left和right指向的struct node可能还有其他左子节点和右子节点,所以我们应该将它们视为子树而不是子节点。
根据这个结构,每棵树都是由以下组合而成的
- 一个带有数据的节点
- 两个子树
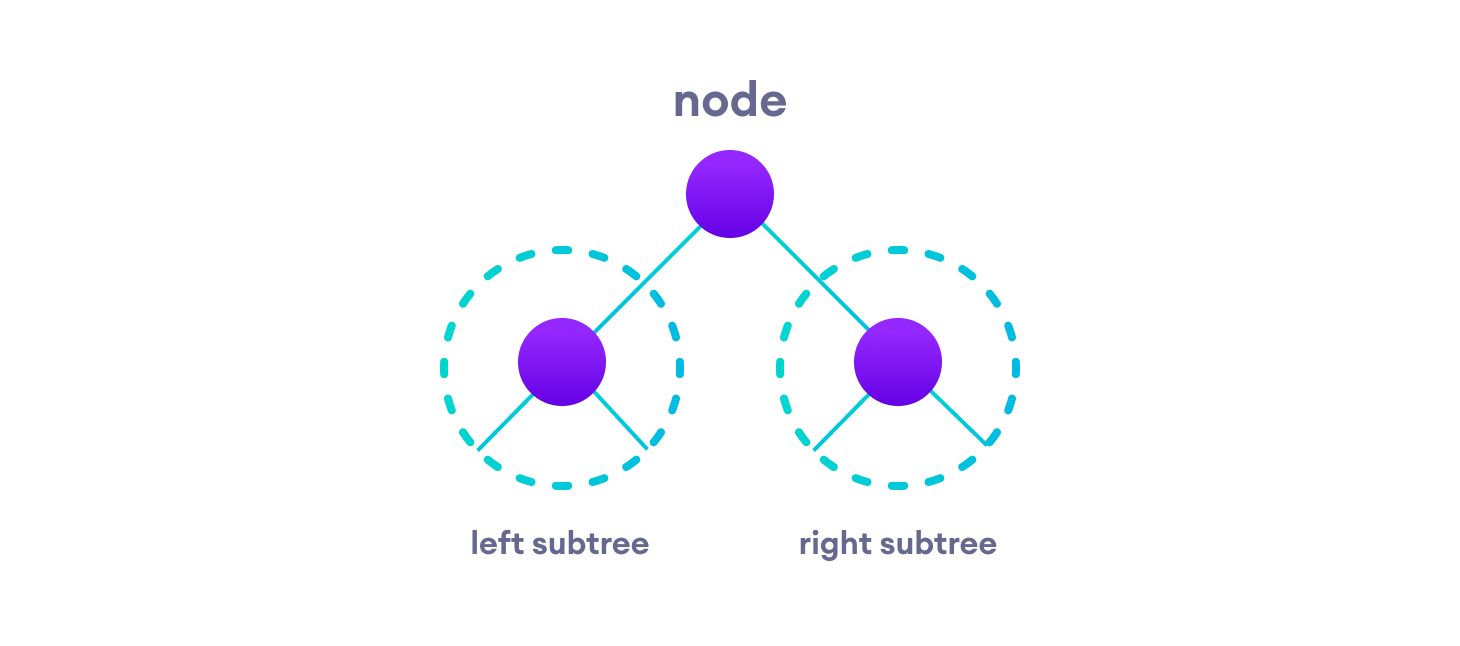
请记住,我们的目标是访问每个节点,所以我们需要访问子树中的所有节点,访问根节点,然后再访问右子树中的所有节点。
根据我们执行此操作的顺序,可以有三种类型的遍历。
中序遍历
- 首先,访问左子树中的所有节点
- 然后是根节点
- 访问右子树中的所有节点
inorder(root->left)
display(root->data)
inorder(root->right)前序遍历
- 访问根节点
- 访问左子树中的所有节点
- 访问右子树中的所有节点
display(root->data)
preorder(root->left)
preorder(root->right)后序遍历
- 访问左子树中的所有节点
- 访问右子树中的所有节点
- 访问根节点
postorder(root->left)
postorder(root->right)
display(root->data)让我们来可视化中序遍历。我们从根节点开始。
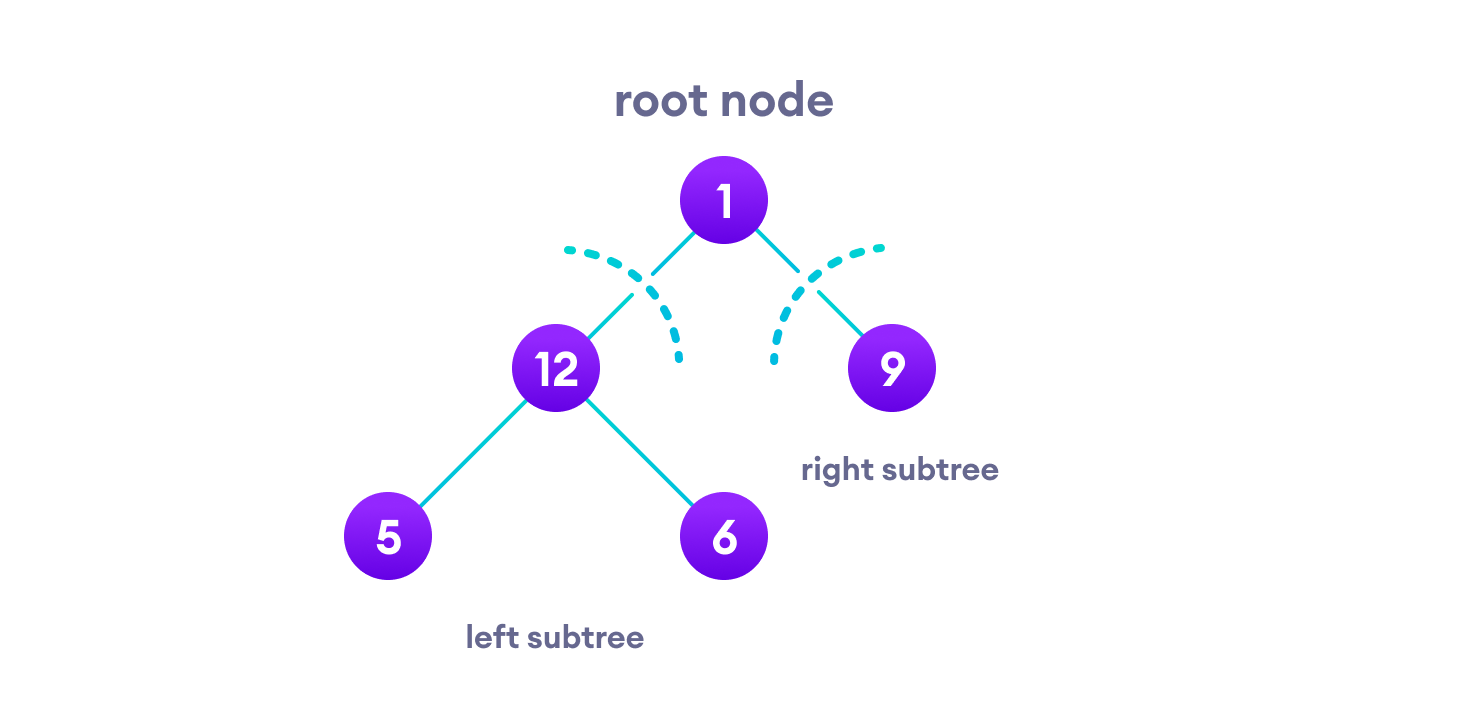
我们首先遍历左子树。当我们完成这棵树时,我们还需要记住访问根节点和右子树。
让我们将所有这些放入栈中,以便我们记住。
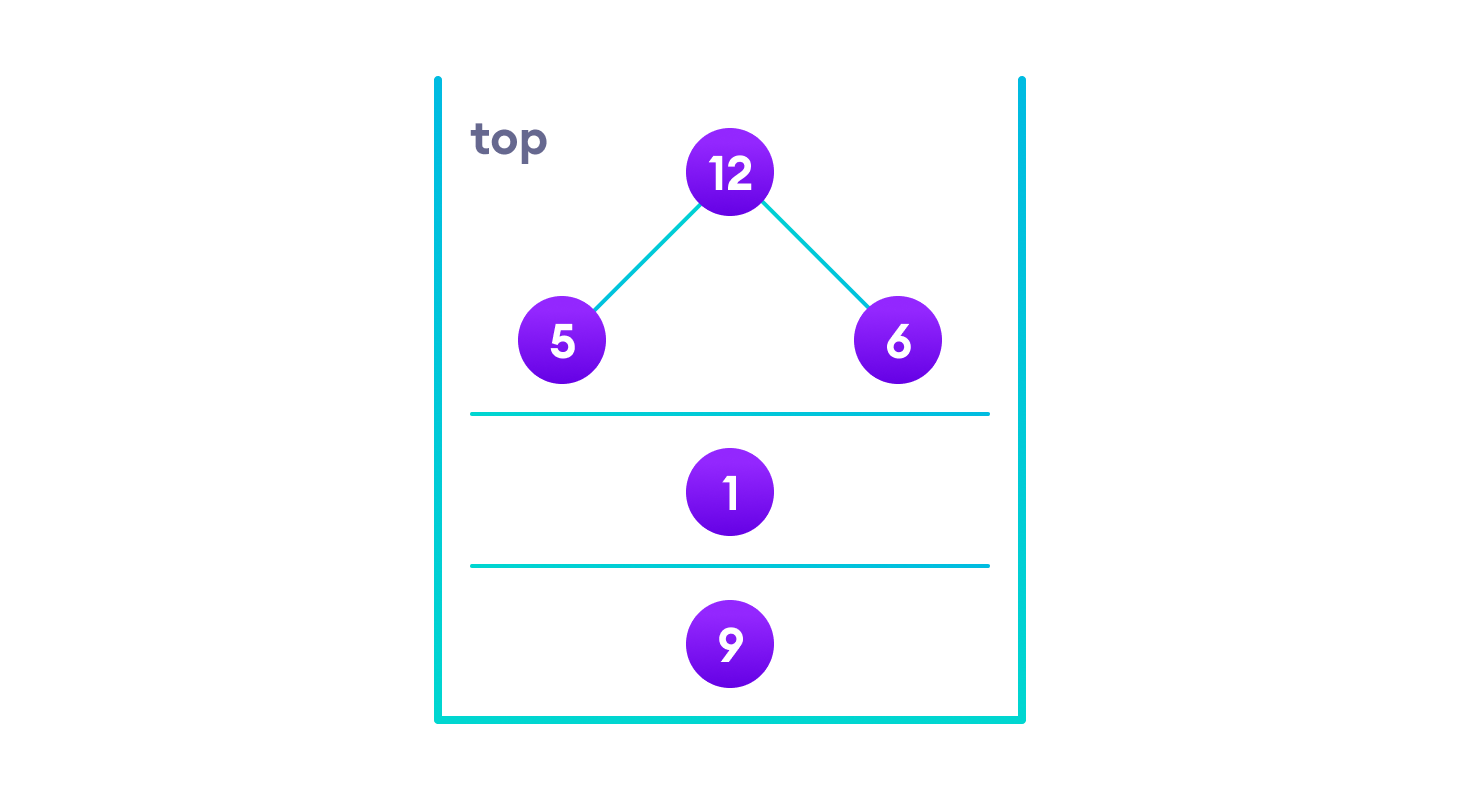
现在我们遍历栈顶的子树。
同样,我们遵循中序遍历的相同规则。
Left subtree -> root -> right subtree
遍历左子树后,我们剩下
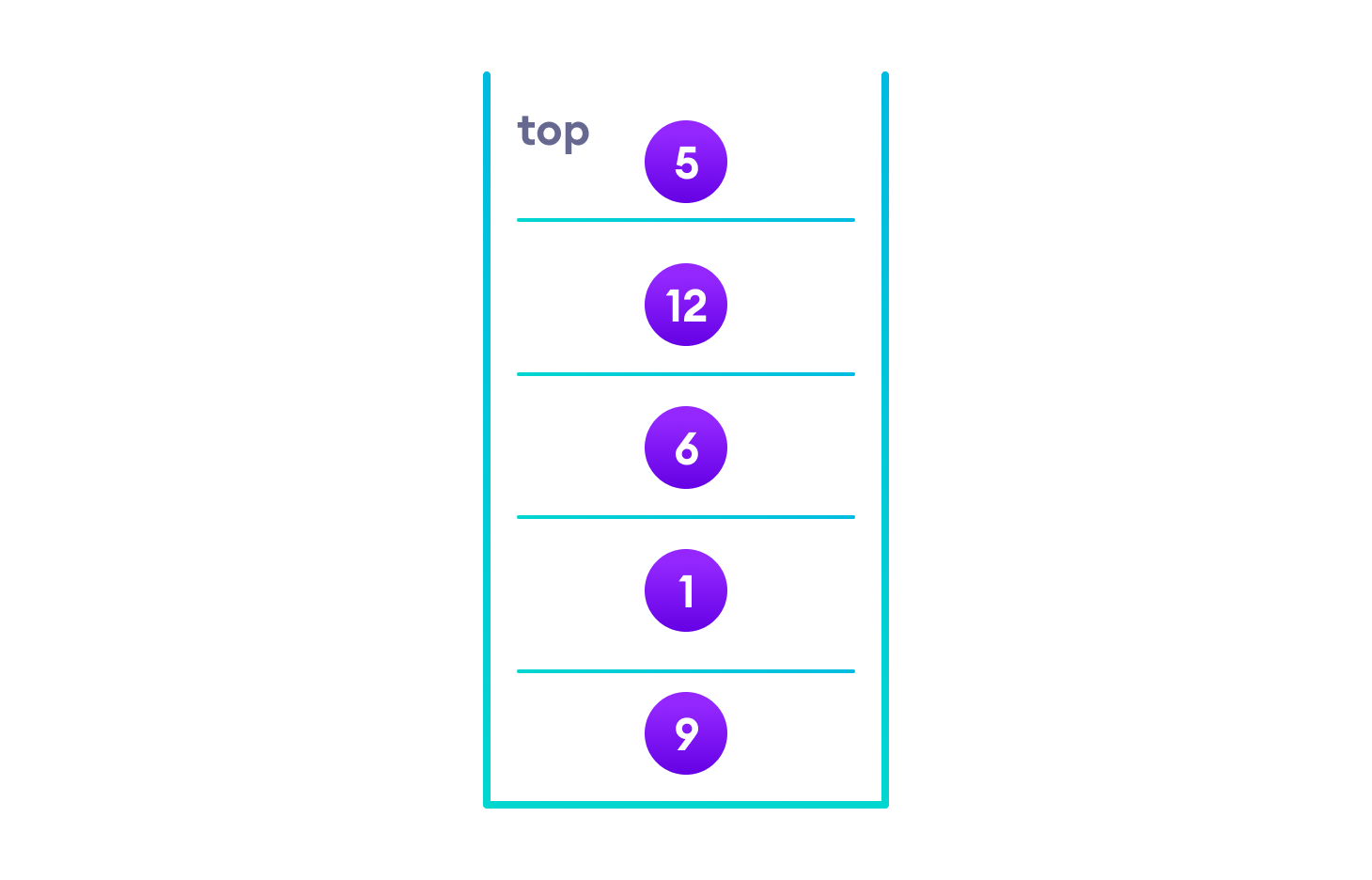
由于节点“5”没有任何子树,我们直接打印它。之后,我们打印它的父节点“12”,然后是右子节点“6”。
将所有内容放入栈中很有帮助,因为现在根节点的左子树已经遍历完成,我们可以打印它并转到右子树。
遍历完所有元素后,我们得到中序遍历结果为
5 -> 12 -> 6 -> 1 -> 9
我们不必自己创建栈,因为递归会为我们维护正确的顺序。
Python、Java 和 C/C++ 示例
# Tree traversal in Python
class Node:
def __init__(self, item):
self.left = None
self.right = None
self.val = item
def inorder(root):
if root:
# Traverse left
inorder(root.left)
# Traverse root
print(str(root.val) + "->", end='')
# Traverse right
inorder(root.right)
def postorder(root):
if root:
# Traverse left
postorder(root.left)
# Traverse right
postorder(root.right)
# Traverse root
print(str(root.val) + "->", end='')
def preorder(root):
if root:
# Traverse root
print(str(root.val) + "->", end='')
# Traverse left
preorder(root.left)
# Traverse right
preorder(root.right)
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("Inorder traversal ")
inorder(root)
print("\nPreorder traversal ")
preorder(root)
print("\nPostorder traversal ")
postorder(root)// Tree traversal in Java
class Node {
int item;
Node left, right;
public Node(int key) {
item = key;
left = right = null;
}
}
class BinaryTree {
// Root of Binary Tree
Node root;
BinaryTree() {
root = null;
}
void postorder(Node node) {
if (node == null)
return;
// Traverse left
postorder(node.left);
// Traverse right
postorder(node.right);
// Traverse root
System.out.print(node.item + "->");
}
void inorder(Node node) {
if (node == null)
return;
// Traverse left
inorder(node.left);
// Traverse root
System.out.print(node.item + "->");
// Traverse right
inorder(node.right);
}
void preorder(Node node) {
if (node == null)
return;
// Traverse root
System.out.print(node.item + "->");
// Traverse left
preorder(node.left);
// Traverse right
preorder(node.right);
}
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(12);
tree.root.right = new Node(9);
tree.root.left.left = new Node(5);
tree.root.left.right = new Node(6);
System.out.println("Inorder traversal");
tree.inorder(tree.root);
System.out.println("\nPreorder traversal ");
tree.preorder(tree.root);
System.out.println("\nPostorder traversal");
tree.postorder(tree.root);
}
}// Tree traversal in C
#include <stdio.h>
#include <stdlib.h>
struct node {
int item;
struct node* left;
struct node* right;
};
// Inorder traversal
void inorderTraversal(struct node* root) {
if (root == NULL) return;
inorderTraversal(root->left);
printf("%d ->", root->item);
inorderTraversal(root->right);
}
// preorderTraversal traversal
void preorderTraversal(struct node* root) {
if (root == NULL) return;
printf("%d ->", root->item);
preorderTraversal(root->left);
preorderTraversal(root->right);
}
// postorderTraversal traversal
void postorderTraversal(struct node* root) {
if (root == NULL) return;
postorderTraversal(root->left);
postorderTraversal(root->right);
printf("%d ->", root->item);
}
// Create a new Node
struct node* createNode(value) {
struct node* newNode = malloc(sizeof(struct node));
newNode->item = value;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// Insert on the left of the node
struct node* insertLeft(struct node* root, int value) {
root->left = createNode(value);
return root->left;
}
// Insert on the right of the node
struct node* insertRight(struct node* root, int value) {
root->right = createNode(value);
return root->right;
}
int main() {
struct node* root = createNode(1);
insertLeft(root, 12);
insertRight(root, 9);
insertLeft(root->left, 5);
insertRight(root->left, 6);
printf("Inorder traversal \n");
inorderTraversal(root);
printf("\nPreorder traversal \n");
preorderTraversal(root);
printf("\nPostorder traversal \n");
postorderTraversal(root);
}// Tree traversal in C++
#include <iostream>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
Node(int data) {
this->data = data;
left = right = NULL;
}
};
// Preorder traversal
void preorderTraversal(struct Node* node) {
if (node == NULL)
return;
cout << node->data << "->";
preorderTraversal(node->left);
preorderTraversal(node->right);
}
// Postorder traversal
void postorderTraversal(struct Node* node) {
if (node == NULL)
return;
postorderTraversal(node->left);
postorderTraversal(node->right);
cout << node->data << "->";
}
// Inorder traversal
void inorderTraversal(struct Node* node) {
if (node == NULL)
return;
inorderTraversal(node->left);
cout << node->data << "->";
inorderTraversal(node->right);
}
int main() {
struct Node* root = new Node(1);
root->left = new Node(12);
root->right = new Node(9);
root->left->left = new Node(5);
root->left->right = new Node(6);
cout << "Inorder traversal ";
inorderTraversal(root);
cout << "\nPreorder traversal ";
preorderTraversal(root);
cout << "\nPostorder traversal ";
postorderTraversal(root);
return 0;
} 