邻接矩阵是一种将图表示为布尔值(0 或 1)矩阵的方法。有限图可以在计算机中以方阵的形式表示,其中布尔值表示两个顶点之间是否存在直接路径。
例如,我们有一个下面的图。
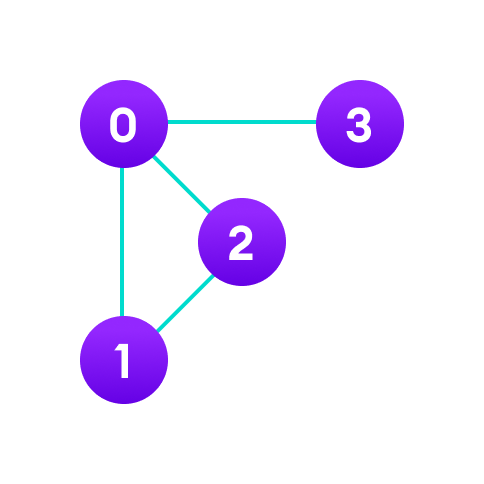
我们可以将此图以矩阵形式表示如下。
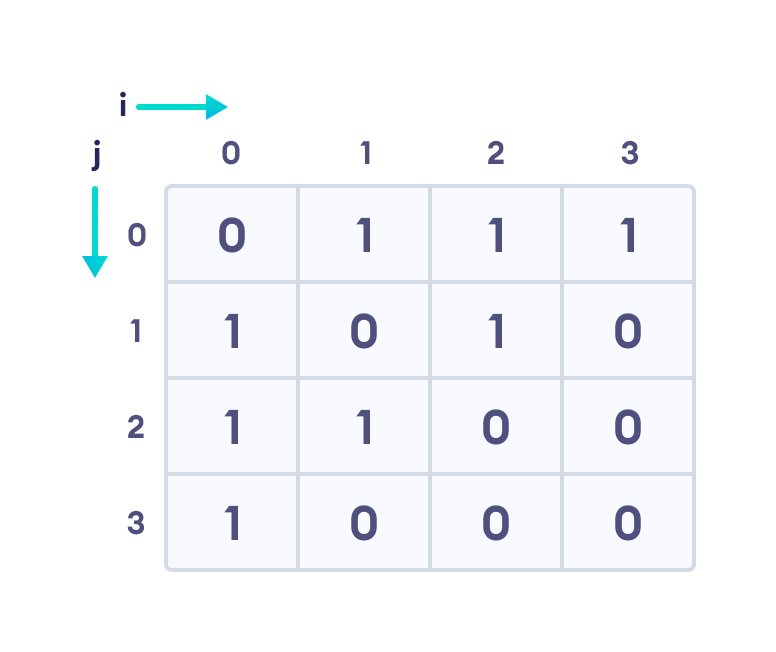
上表/矩阵中的每个单元格表示为Aij,其中i和j是顶点。Aij的值为 1 或 0,取决于从顶点i到顶点j是否存在边。
如果从i到j存在路径,则Aij的值为 1,否则为 0。例如,从顶点 1 到顶点 2 存在路径,因此A12为 1,而从顶点 1 到顶点 3 不存在路径,因此A13为 0。
对于无向图,矩阵关于对角线是对称的,因为每条边(i,j)都存在一条边(j,i)。
邻接矩阵的优点
- 诸如添加边、删除边以及检查从顶点 i 到顶点 j 是否存在边等基本操作具有极高的时间效率,是常数时间操作。
- 如果图是稠密的且边数很多,邻接矩阵应该是首选。即使图和邻接矩阵是稀疏的,我们也可以使用稀疏矩阵的数据结构来表示它。
- 然而,最大的优势来自于矩阵的使用。最近的硬件进步使我们能够在 GPU 上执行复杂的矩阵运算。
- 通过对邻接矩阵进行操作,我们可以深入了解图的性质及其顶点之间的关系。
邻接矩阵的缺点
- 邻接矩阵的
VxV空间需求使其成为内存占用大户。现实世界中的图通常连接不多,这就是为什么对于大多数任务而言,邻接表是更好的选择。 - 虽然基本操作很简单,但使用邻接矩阵表示时,诸如
inEdges(入边)和outEdges(出边)之类的操作会很耗时。
Python、Java 和 C/C++ 中的邻接矩阵代码
如果你知道如何创建二维数组,那么你也知道如何创建邻接矩阵。
# Adjacency Matrix representation in Python
class Graph(object):
# Initialize the matrix
def __init__(self, size):
self.adjMatrix = []
for i in range(size):
self.adjMatrix.append([0 for i in range(size)])
self.size = size
# Add edges
def add_edge(self, v1, v2):
if v1 == v2:
print("Same vertex %d and %d" % (v1, v2))
self.adjMatrix[v1][v2] = 1
self.adjMatrix[v2][v1] = 1
# Remove edges
def remove_edge(self, v1, v2):
if self.adjMatrix[v1][v2] == 0:
print("No edge between %d and %d" % (v1, v2))
return
self.adjMatrix[v1][v2] = 0
self.adjMatrix[v2][v1] = 0
def __len__(self):
return self.size
# Print the matrix
def print_matrix(self):
for row in self.adjMatrix:
for val in row:
print('{:4}'.format(val)),
print
def main():
g = Graph(5)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(2, 3)
g.print_matrix()
if __name__ == '__main__':
main()// Adjacency Matrix representation in Java
public class Graph {
private boolean adjMatrix[][];
private int numVertices;
// Initialize the matrix
public Graph(int numVertices) {
this.numVertices = numVertices;
adjMatrix = new boolean[numVertices][numVertices];
}
// Add edges
public void addEdge(int i, int j) {
adjMatrix[i][j] = true;
adjMatrix[j][i] = true;
}
// Remove edges
public void removeEdge(int i, int j) {
adjMatrix[i][j] = false;
adjMatrix[j][i] = false;
}
// Print the matrix
public String toString() {
StringBuilder s = new StringBuilder();
for (int i = 0; i < numVertices; i++) {
s.append(i + ": ");
for (boolean j : adjMatrix[i]) {
s.append((j ? 1 : 0) + " ");
}
s.append("\n");
}
return s.toString();
}
public static void main(String args[]) {
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
System.out.print(g.toString());
}
}// Adjacency Matrix representation in C
#include <stdio.h>
#define V 4
// Initialize the matrix to zero
void init(int arr[][V]) {
int i, j;
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
arr[i][j] = 0;
}
// Add edges
void addEdge(int arr[][V], int i, int j) {
arr[i][j] = 1;
arr[j][i] = 1;
}
// Print the matrix
void printAdjMatrix(int arr[][V]) {
int i, j;
for (i = 0; i < V; i++) {
printf("%d: ", i);
for (j = 0; j < V; j++) {
printf("%d ", arr[i][j]);
}
printf("\n");
}
}
int main() {
int adjMatrix[V][V];
init(adjMatrix);
addEdge(adjMatrix, 0, 1);
addEdge(adjMatrix, 0, 2);
addEdge(adjMatrix, 1, 2);
addEdge(adjMatrix, 2, 0);
addEdge(adjMatrix, 2, 3);
printAdjMatrix(adjMatrix);
return 0;
}// Adjacency Matrix representation in C++
#include <iostream>
using namespace std;
class Graph {
private:
bool** adjMatrix;
int numVertices;
public:
// Initialize the matrix to zero
Graph(int numVertices) {
this->numVertices = numVertices;
adjMatrix = new bool*[numVertices];
for (int i = 0; i < numVertices; i++) {
adjMatrix[i] = new bool[numVertices];
for (int j = 0; j < numVertices; j++)
adjMatrix[i][j] = false;
}
}
// Add edges
void addEdge(int i, int j) {
adjMatrix[i][j] = true;
adjMatrix[j][i] = true;
}
// Remove edges
void removeEdge(int i, int j) {
adjMatrix[i][j] = false;
adjMatrix[j][i] = false;
}
// Print the martix
void toString() {
for (int i = 0; i < numVertices; i++) {
cout << i << " : ";
for (int j = 0; j < numVertices; j++)
cout << adjMatrix[i][j] << " ";
cout << "\n";
}
}
~Graph() {
for (int i = 0; i < numVertices; i++)
delete[] adjMatrix[i];
delete[] adjMatrix;
}
};
int main() {
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.toString();
}邻接矩阵的应用
- 在网络中创建路由表
- 导航任务
