强连通分量是指有向图的一部分,其中每个顶点都可以到达另一个顶点。**它仅适用于**有向图。
例如
我们以下面的图为例。
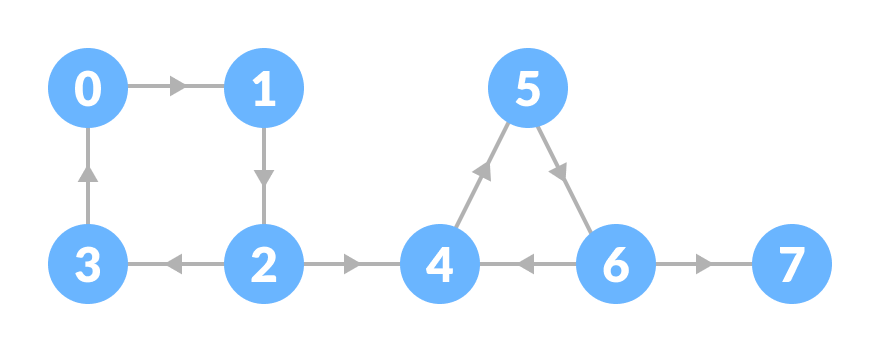
上述图的强连通分量是
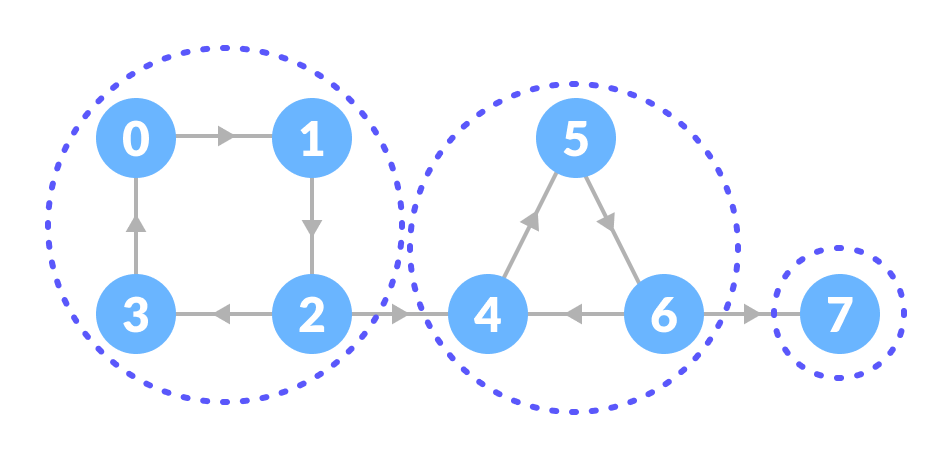
您会发现,在第一个强连通分量中,每个顶点都可以通过有向路径到达其他顶点。
可以使用**Kosaraju 算法**找到这些分量。
Kosaraju 算法
Kosaraju 算法基于深度优先搜索算法,并执行两次。
涉及三个步骤。
- 对整个图执行深度优先搜索。
让我们从顶点 0 开始,访问其所有子顶点,并将访问过的顶点标记为已完成。如果一个顶点导向一个已访问过的顶点,则将该顶点推入栈。
例如:从顶点 0 开始,前往顶点 1,顶点 2,然后到顶点 3。顶点 3 指向已访问过的顶点 0,因此将源顶点(即顶点 3)推入栈。
图的 DFS
转到上一个顶点(顶点 2),并依次访问其子顶点,即顶点 4、顶点 5、顶点 6 和顶点 7。由于从顶点 7 无处可去,因此将其推入栈。
图的 DFS
转到上一个顶点(顶点 6),并访问其子顶点。但是,其所有子顶点都已被访问,因此将其推入栈。
堆叠
类似地,会创建一个最终栈。
最终栈 - 反转原始图。

反向图的 DFS - 对反向图执行深度优先搜索。
从栈顶顶点开始。遍历其所有子顶点。一旦到达已访问过的顶点,就形成了一个强连通分量。
例如:从栈中弹出顶点 0。从顶点 0 开始,遍历其子顶点(按顺序为顶点 0、顶点 1、顶点 2、顶点 3),并将其标记为已访问。顶点 3 的子节点已被访问,因此这些已访问的顶点构成一个强连通分量。
从顶部开始,遍历所有顶点
转到栈并弹出已访问的顶点。否则,选择栈顶顶点并遍历其子顶点,如上所述。
弹出已访问的顶点 
强连通分量 - 因此,强连通分量是

所有强连通分量
Python、Java、C++ 示例
# Kosaraju's algorithm to find strongly connected components in Python
from collections import defaultdict
class Graph:
def __init__(self, vertex):
self.V = vertex
self.graph = defaultdict(list)
# Add edge into the graph
def add_edge(self, s, d):
self.graph[s].append(d)
# dfs
def dfs(self, d, visited_vertex):
visited_vertex[d] = True
print(d, end='')
for i in self.graph[d]:
if not visited_vertex[i]:
self.dfs(i, visited_vertex)
def fill_order(self, d, visited_vertex, stack):
visited_vertex[d] = True
for i in self.graph[d]:
if not visited_vertex[i]:
self.fill_order(i, visited_vertex, stack)
stack = stack.append(d)
# transpose the matrix
def transpose(self):
g = Graph(self.V)
for i in self.graph:
for j in self.graph[i]:
g.add_edge(j, i)
return g
# Print stongly connected components
def print_scc(self):
stack = []
visited_vertex = [False] * (self.V)
for i in range(self.V):
if not visited_vertex[i]:
self.fill_order(i, visited_vertex, stack)
gr = self.transpose()
visited_vertex = [False] * (self.V)
while stack:
i = stack.pop()
if not visited_vertex[i]:
gr.dfs(i, visited_vertex)
print("")
g = Graph(8)
g.add_edge(0, 1)
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(2, 4)
g.add_edge(3, 0)
g.add_edge(4, 5)
g.add_edge(5, 6)
g.add_edge(6, 4)
g.add_edge(6, 7)
print("Strongly Connected Components:")
g.print_scc()// Kosaraju's algorithm to find strongly connected components in Java
import java.util.*;
import java.util.LinkedList;
class Graph {
private int V;
private LinkedList<Integer> adj[];
// Create a graph
Graph(int s) {
V = s;
adj = new LinkedList[s];
for (int i = 0; i < s; ++i)
adj[i] = new LinkedList();
}
// Add edge
void addEdge(int s, int d) {
adj[s].add(d);
}
// DFS
void DFSUtil(int s, boolean visitedVertices[]) {
visitedVertices[s] = true;
System.out.print(s + " ");
int n;
Iterator<Integer> i = adj[s].iterator();
while (i.hasNext()) {
n = i.next();
if (!visitedVertices[n])
DFSUtil(n, visitedVertices);
}
}
// Transpose the graph
Graph Transpose() {
Graph g = new Graph(V);
for (int s = 0; s < V; s++) {
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext())
g.adj[i.next()].add(s);
}
return g;
}
void fillOrder(int s, boolean visitedVertices[], Stack stack) {
visitedVertices[s] = true;
Iterator<Integer> i = adj[s].iterator();
while (i.hasNext()) {
int n = i.next();
if (!visitedVertices[n])
fillOrder(n, visitedVertices, stack);
}
stack.push(new Integer(s));
}
// Print strongly connected component
void printSCC() {
Stack stack = new Stack();
boolean visitedVertices[] = new boolean[V];
for (int i = 0; i < V; i++)
visitedVertices[i] = false;
for (int i = 0; i < V; i++)
if (visitedVertices[i] == false)
fillOrder(i, visitedVertices, stack);
Graph gr = Transpose();
for (int i = 0; i < V; i++)
visitedVertices[i] = false;
while (stack.empty() == false) {
int s = (int) stack.pop();
if (visitedVertices[s] == false) {
gr.DFSUtil(s, visitedVertices);
System.out.println();
}
}
}
public static void main(String args[]) {
Graph g = new Graph(8);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 3);
g.addEdge(2, 4);
g.addEdge(3, 0);
g.addEdge(4, 5);
g.addEdge(5, 6);
g.addEdge(6, 4);
g.addEdge(6, 7);
System.out.println("Strongly Connected Components:");
g.printSCC();
}
}// Kosaraju's algorithm to find strongly connected components in C++
#include <iostream>
#include <list>
#include <stack>
using namespace std;
class Graph {
int V;
list<int> *adj;
void fillOrder(int s, bool visitedV[], stack<int> &Stack);
void DFS(int s, bool visitedV[]);
public:
Graph(int V);
void addEdge(int s, int d);
void printSCC();
Graph transpose();
};
Graph::Graph(int V) {
this->V = V;
adj = new list<int>[V];
}
// DFS
void Graph::DFS(int s, bool visitedV[]) {
visitedV[s] = true;
cout << s << " ";
list<int>::iterator i;
for (i = adj[s].begin(); i != adj[s].end(); ++i)
if (!visitedV[*i])
DFS(*i, visitedV);
}
// Transpose
Graph Graph::transpose() {
Graph g(V);
for (int s = 0; s < V; s++) {
list<int>::iterator i;
for (i = adj[s].begin(); i != adj[s].end(); ++i) {
g.adj[*i].push_back(s);
}
}
return g;
}
// Add edge into the graph
void Graph::addEdge(int s, int d) {
adj[s].push_back(d);
}
void Graph::fillOrder(int s, bool visitedV[], stack<int> &Stack) {
visitedV[s] = true;
list<int>::iterator i;
for (i = adj[s].begin(); i != adj[s].end(); ++i)
if (!visitedV[*i])
fillOrder(*i, visitedV, Stack);
Stack.push(s);
}
// Print strongly connected component
void Graph::printSCC() {
stack<int> Stack;
bool *visitedV = new bool[V];
for (int i = 0; i < V; i++)
visitedV[i] = false;
for (int i = 0; i < V; i++)
if (visitedV[i] == false)
fillOrder(i, visitedV, Stack);
Graph gr = transpose();
for (int i = 0; i < V; i++)
visitedV[i] = false;
while (Stack.empty() == false) {
int s = Stack.top();
Stack.pop();
if (visitedV[s] == false) {
gr.DFS(s, visitedV);
cout << endl;
}
}
}
int main() {
Graph g(8);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 3);
g.addEdge(2, 4);
g.addEdge(3, 0);
g.addEdge(4, 5);
g.addEdge(5, 6);
g.addEdge(6, 4);
g.addEdge(6, 7);
cout << "Strongly Connected Components:\n";
g.printSCC();
}Kosaraju 算法复杂度
Kosaraju 算法以线性时间运行,即 `O(V+E)`。
强连通分量的应用
- 车辆路径规划应用
- 地图
- 形式化验证中的模型检查









