贪心算法是一种通过在当前时刻选择最佳选项来解决问题的策略。它不关心当前的最佳结果是否能带来整体的最优结果。
该算法一旦做出选择,即使是错误的,也不会撤销之前的决定。它以自顶向下的方式工作。
对于所有问题,该算法可能无法产生最佳结果。这是因为它总是追求局部最优选择来产生全局最优结果。
但是,我们可以确定该算法是否可用于任何问题,前提是该问题具有以下属性
1. 贪心选择性质
如果通过在每一步选择最佳选项而不重新考虑已选择的先前步骤即可找到问题的最优解,则可以使用贪心方法解决该问题。此属性称为贪心选择性质。
2. 最优子结构
如果问题的整体最优解对应于其子问题的最优解,则可以使用贪心方法解决该问题。此属性称为最优子结构。
贪心方法的优点
- 该算法易于描述。
- 该算法可以比其他算法表现更好(但并非在所有情况下)。
贪心方法的缺点
如前所述,贪心算法并不总是产生最优解。这是该算法的主要缺点。
例如,假设我们要找到下面图中从根到叶的最长路径。让我们在这里使用贪心算法。
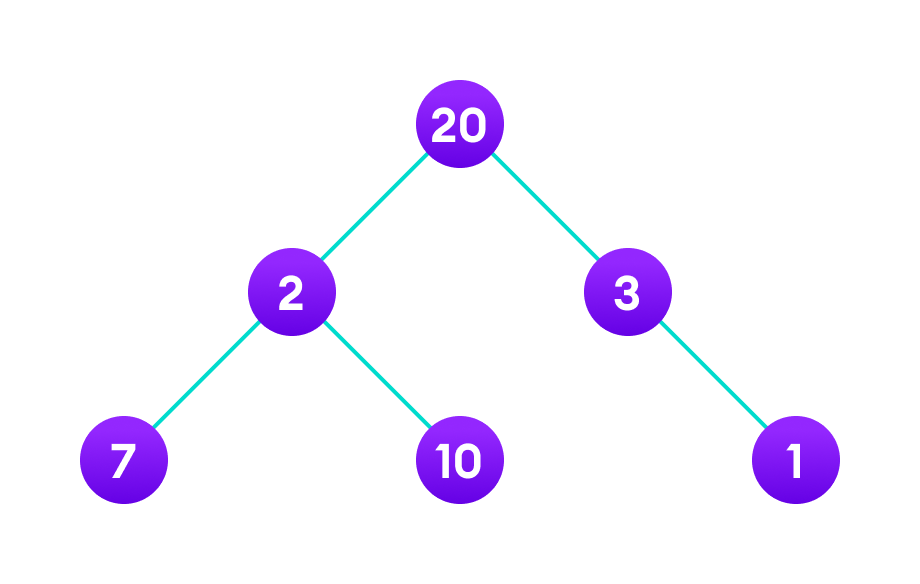
贪心方法
1. 让我们从根节点20开始。右子节点的权重是3,左子节点的权重是2。
2. 我们的问题是找到最大路径。而当前的最佳解决方案是3。因此,贪心算法将选择3。
3. 最后,3的唯一子节点的权重是1。这样我们就得到了最终结果20 + 3 + 1 = 24。
然而,这不是最优解。还有另一条路径携带的权重更大(20 + 2 + 10 = 32),如下图所示。
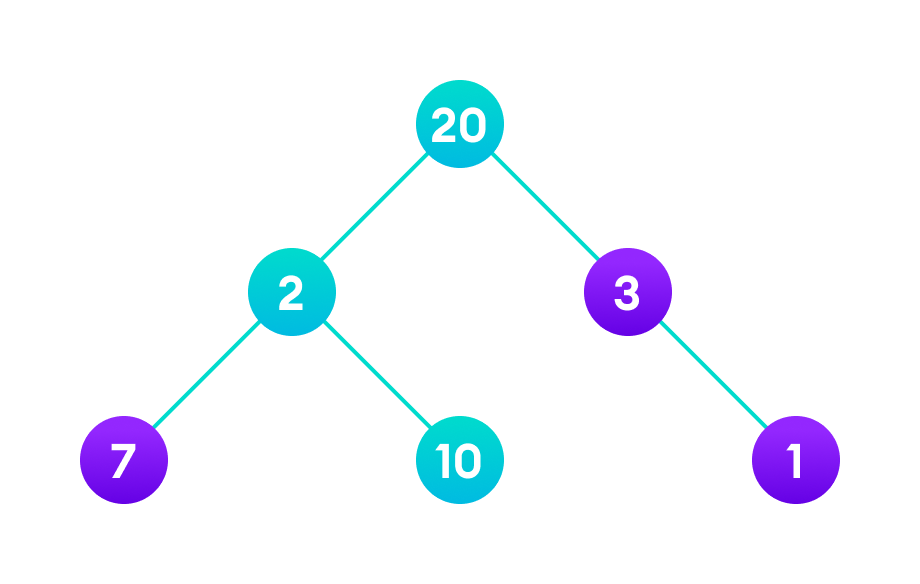
因此,贪心算法并不总是能给出最优/可行的解决方案。
贪婪算法
- 首先,解决方案集(包含答案)为空。
- 在每一步,都会将一个项目添加到解决方案集中,直到达到解决方案。
- 如果解决方案集可行,则保留当前项目。
- 否则,拒绝该项目,且不再考虑。
现在让我们使用此算法来解决一个问题。
示例 - 贪心方法
Problem: You have to make a change of an amount using the smallest possible number of coins. Amount: $18 Available coins are $5 coin $2 coin $1 coin There is no limit to the number of each coin you can use.
解决方案
- 创建一个空的
solution-set = { }。可用硬币是{5, 2, 1}。 - 我们需要找到
sum = 18。让我们从sum = 0开始。 - 始终选择最大值的硬币(即5),直到
sum > 18。(当我们每一步都选择最大值时,我们希望更快地到达目的地。这个概念被称为贪心选择性质。) - 在第一次迭代中,
solution-set = {5},sum = 5。 - 在第二次迭代中,
solution-set = {5, 5},sum = 10。 - 在第三次迭代中,
solution-set = {5, 5, 5},sum = 15。 - 在第四次迭代中,
solution-set = {5, 5, 5, 2},sum = 17。(我们不能在这里选择5,因为如果我们这样做,sum = 20,它大于18。因此,我们选择第二大的项,即2。) - 类似地,在第五次迭代中,选择1。现在
sum = 18,solution-set = {5, 5, 5, 2, 1}。
