分而治之算法是一种通过将一个大问题分解为
- 更小的子问题
- 来解决它的策略,然后
- 将它们组合起来以获得期望的输出。
要使用分而治之算法,通常会使用递归。了解不同编程语言中的递归
想正确学习递归吗?免费报名参加我们的 互动递归课程。
分而治之算法如何工作?
以下是涉及的步骤:
- 分解:使用递归将给定问题分解为子问题。
- 征服:递归地解决较小的子问题。如果子问题足够小,则直接解决它。
- 合并:合并递归过程中子问题的解,以解决实际问题。
让我们通过一个例子来理解这个概念。
在这里,我们将使用分而治之方法(即 归并排序)对数组进行排序。
- 设给定的数组为

用于归并排序的数组 - 分解数组为两半。

将数组分解为两个子部分
再次,递归地将每个子部分分解为两半,直到得到单个元素。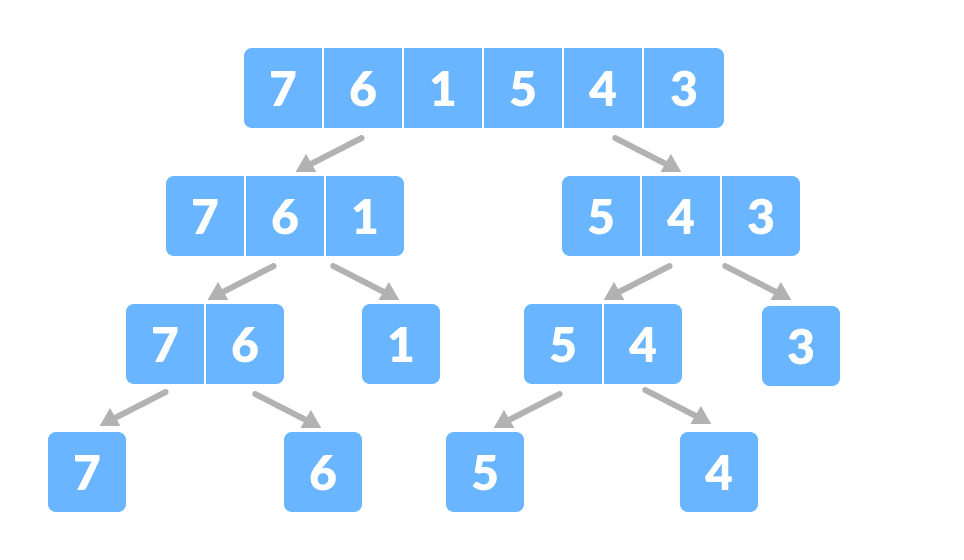
将数组分解为更小的子部分 - 现在,以排序的方式组合单个元素。在这里,征服和合并步骤是并行的。
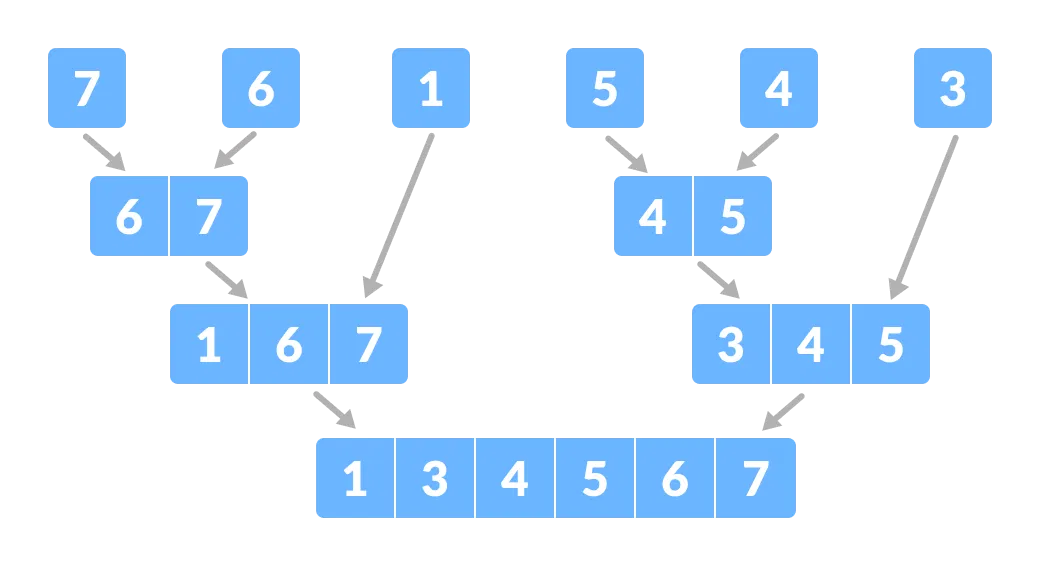
合并子部分
时间复杂度
分而治之算法的复杂度使用 主定理 计算。
T(n) = aT(n/b) + f(n), where, n = size of input a = number of subproblems in the recursion n/b = size of each subproblem. All subproblems are assumed to have the same size. f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions
让我们举一个例子来找出递归问题的时空复杂度。
对于归并排序,方程可以写为
T(n) = aT(n/b) + f(n)
= 2T(n/2) + O(n)
Where,
a = 2 (each time, a problem is divided into 2 subproblems)
n/b = n/2 (size of each sub problem is half of the input)
f(n) = time taken to divide the problem and merging the subproblems
T(n/2) = O(n log n) (To understand this, please refer to the master theorem.)
Now, T(n) = 2T(n log n) + O(n)
≈ O(n log n)
分而治之与动态规划方法
分而治之方法将问题分解为更小的子问题;这些子问题将通过递归进一步解决。每个子问题的结果都不会存储以供将来参考,而在动态规划方法中,每个子问题的结果都会存储以供将来参考。
当同一个子问题不被多次解决时,使用分而治之方法。当子问题的结果将在将来被多次使用时,使用动态规划方法。
让我们通过一个例子来理解这一点。假设我们正在尝试查找斐波那契数列。那么,
分而治之方法
fib(n)
If n < 2, return 1
Else , return f(n - 1) + f(n -2)
动态规划方法
mem = []
fib(n)
If n in mem: return mem[n]
else,
If n < 2, f = 1
else , f = f(n - 1) + f(n -2)
mem[n] = f
return f
在动态规划方法中,mem 存储每个子问题的结果。
分而治之算法的优点
- 使用朴素方法进行两个矩阵乘法的复杂度为 O(n3),而使用分而治之方法(即 Strassen 矩阵乘法)为 O(n2.8074)。这种方法还简化了其他问题,例如汉诺塔。
- 这种方法适用于多处理系统。
- 它能有效地利用内存缓存。
分而治之的应用
想正确学习递归吗?免费报名参加我们的 互动递归课程。




