插入排序是一种排序算法,它在每次迭代中将一个未排序的元素放置到其合适的位置。
插入排序的工作方式与我们在纸牌游戏中整理手中的牌非常相似。
我们假设第一张牌已经排好序,然后选择一张未排序的牌。如果未排序的牌大于手中的牌,则将其放在右边,否则放在左边。同样,取出其他未排序的牌并放在它们正确的位置。
插入排序使用类似的方法。
插入排序的工作原理
假设我们需要对以下数组进行排序。

- 数组中的第一个元素被假定为已排序。取第二个元素并将其单独存储在
key中。
将key与第一个元素进行比较。如果第一个元素大于key,则将 key 放在第一个元素的前面。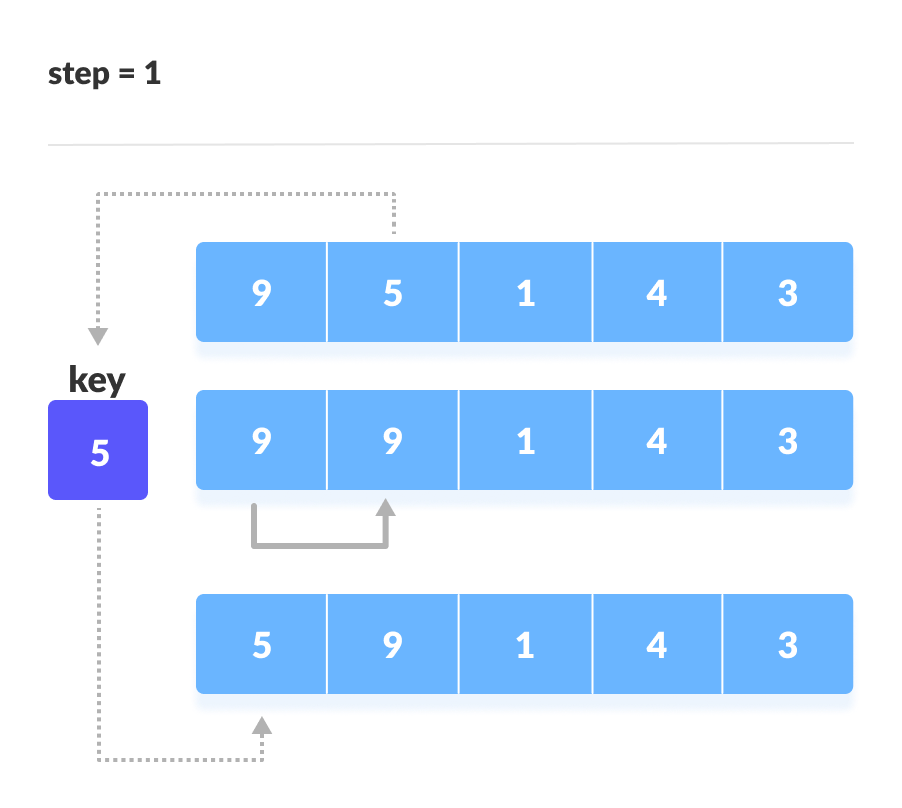
如果第一个元素大于 key,则 key 放在第一个元素的前面。 - 现在,前两个元素已排序。
取第三个元素,并将其与它左边的元素进行比较。将其放在比它小的元素后面。如果没有比它小的元素,则将其放在数组的开头。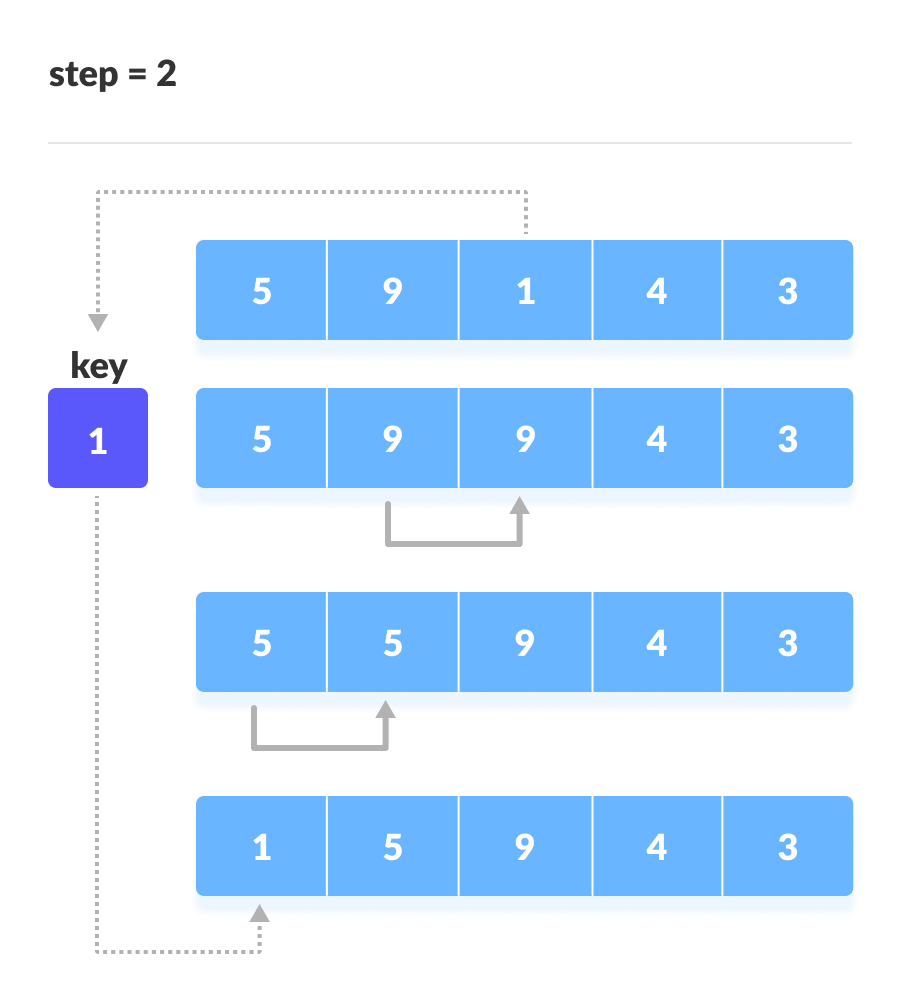
将 1 放在开头 - 类似地,将每个未排序的元素放在其正确的位置。
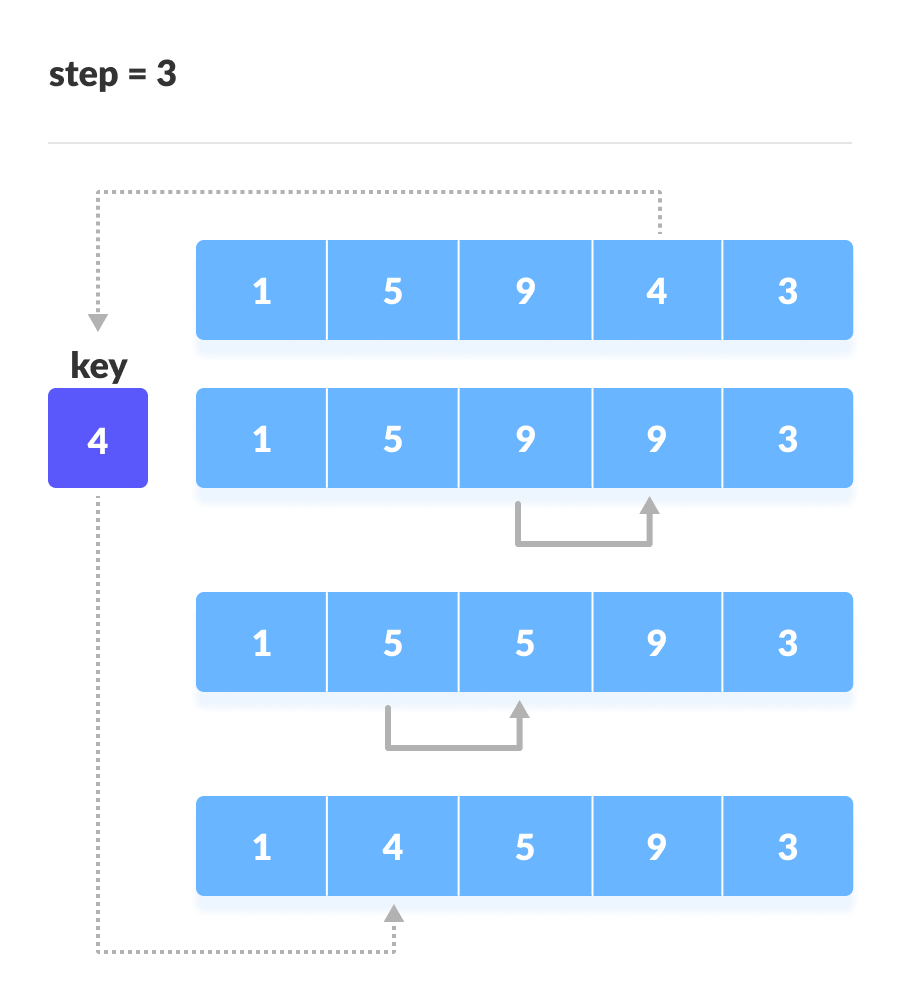
将 4 放在 1 后面 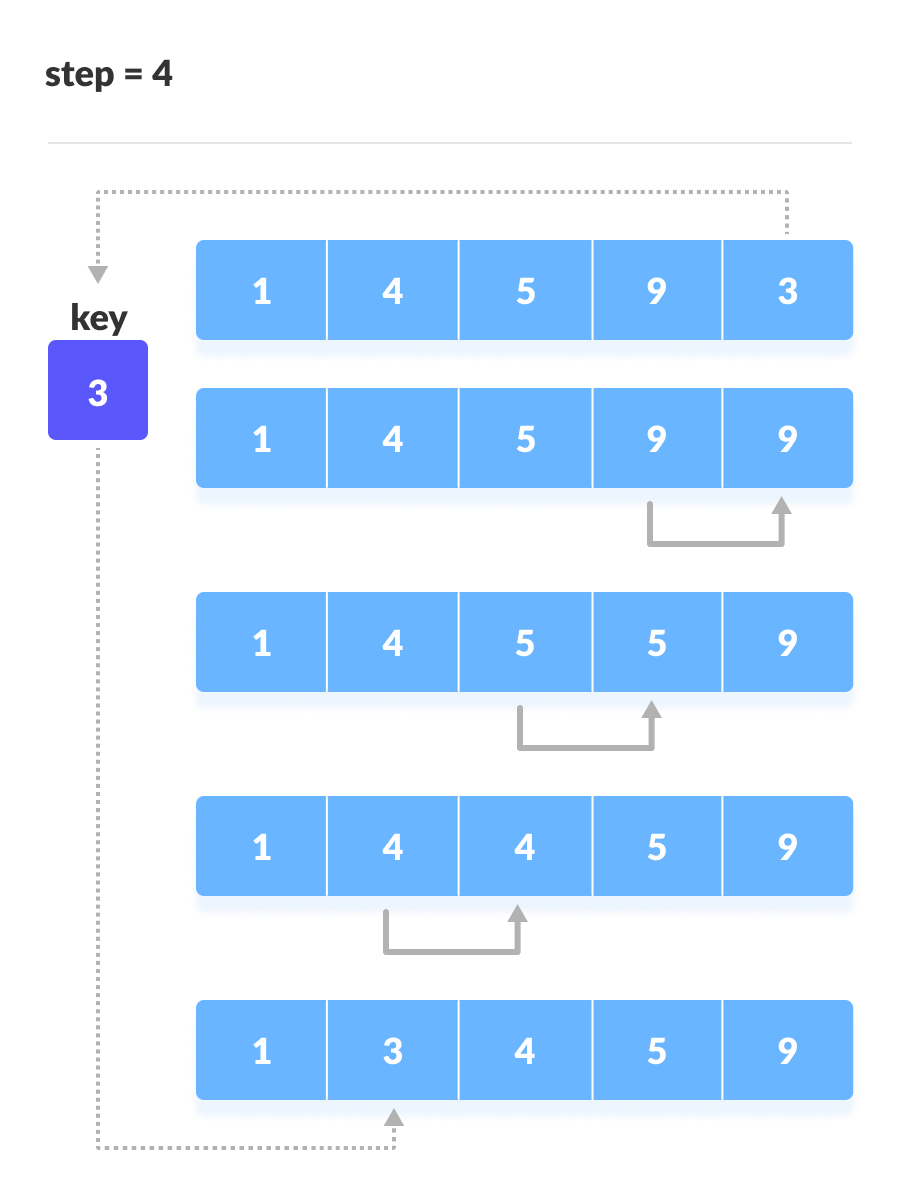
将 3 放在 1 后面,数组已排序
插入排序算法
insertionSort(array)
mark first element as sorted
for each unsorted element X
'extract' the element X
for j <- lastSortedIndex down to 0
if current element j > X
move sorted element to the right by 1
break loop and insert X here
end insertionSortPython、Java 和 C/C++ 中的插入排序
# Insertion sort in Python
def insertionSort(array):
for step in range(1, len(array)):
key = array[step]
j = step - 1
# Compare key with each element on the left of it until an element smaller than it is found
# For descending order, change key<array[j] to key>array[j].
while j >= 0 and key < array[j]:
array[j + 1] = array[j]
j = j - 1
# Place key at after the element just smaller than it.
array[j + 1] = key
data = [9, 5, 1, 4, 3]
insertionSort(data)
print('Sorted Array in Ascending Order:')
print(data)// Insertion sort in Java
import java.util.Arrays;
class InsertionSort {
void insertionSort(int array[]) {
int size = array.length;
for (int step = 1; step < size; step++) {
int key = array[step];
int j = step - 1;
// Compare key with each element on the left of it until an element smaller than
// it is found.
// For descending order, change key<array[j] to key>array[j].
while (j >= 0 && key < array[j]) {
array[j + 1] = array[j];
--j;
}
// Place key at after the element just smaller than it.
array[j + 1] = key;
}
}
// Driver code
public static void main(String args[]) {
int[] data = { 9, 5, 1, 4, 3 };
InsertionSort is = new InsertionSort();
is.insertionSort(data);
System.out.println("Sorted Array in Ascending Order: ");
System.out.println(Arrays.toString(data));
}
}// Insertion sort in C
#include <stdio.h>
// Function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; i++) {
printf("%d ", array[i]);
}
printf("\n");
}
void insertionSort(int array[], int size) {
for (int step = 1; step < size; step++) {
int key = array[step];
int j = step - 1;
// Compare key with each element on the left of it until an element smaller than
// it is found.
// For descending order, change key<array[j] to key>array[j].
while (j >=0 && key < array[j]) {
array[j + 1] = array[j];
--j;
}
array[j + 1] = key;
}
}
// Driver code
int main() {
int data[] = {9, 5, 1, 4, 3};
int size = sizeof(data) / sizeof(data[0]);
insertionSort(data, size);
printf("Sorted array in ascending order:\n");
printArray(data, size);
}// Insertion sort in C++
#include <iostream>
using namespace std;
// Function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; i++) {
cout << array[i] << " ";
}
cout << endl;
}
void insertionSort(int array[], int size) {
for (int step = 1; step < size; step++) {
int key = array[step];
int j = step - 1;
// Compare key with each element on the left of it until an element smaller than
// it is found.
// For descending order, change key<array[j] to key>array[j].
while (j >=0 && key < array[j]) {
array[j + 1] = array[j];
--j;
}
array[j + 1] = key;
}
}
// Driver code
int main() {
int data[] = {9, 5, 1, 4, 3};
int size = sizeof(data) / sizeof(data[0]);
insertionSort(data, size);
cout << "Sorted array in ascending order:\n";
printArray(data, size);
}插入排序复杂度
| 时间复杂度 | |
|---|---|
| 最佳 | O(n) |
| 最差 | O(n2) |
| 平均 | O(n2) |
| 空间复杂度 | O(1) |
| 稳定性 | 是 |
时间复杂度
- 最坏情况复杂度:
O(n2)
假设一个数组是升序排列的,而您想将其降序排列。在这种情况下,会出现最坏情况复杂度。
每个元素都必须与所有其他元素进行比较,因此对于每个第 n 个元素,会进行(n-1)次比较。
因此,总比较次数 =n*(n-1) ~ n2 - 最佳情况复杂度:
O(n)
当数组已排序时,外循环运行 n 次,而内循环根本不运行。因此,只有 n 次比较。因此,复杂度是线性的。 - 平均情况复杂度:
O(n2)
当数组元素的顺序混乱时(既不升序也不降序)会发生这种情况。
空间复杂度
由于使用了额外的变量 key,因此空间复杂度为 O(1)。
插入排序的应用
插入排序用于
- 数组中的元素数量很少
- 只有少数元素需要排序
