遍历是指访问图的所有节点。广度优先遍历或广度优先搜索是一种用于搜索图或树数据结构的所有顶点的递归算法。
BFS 算法
标准的 BFS 实现将图的每个顶点分为两类:
- 已访问
- 未访问
该算法的目的是标记每个顶点为已访问,同时避免循环。
算法工作如下:
- 首先,将图的任意一个顶点放入队列的末尾。
- 取出队列的第一个元素并将其添加到已访问列表中。
- 列出该顶点的邻接节点。将不在已访问列表中的节点添加到队列的末尾。
- 重复步骤 2 和 3,直到队列为空。
图可能有两个不同的不连通部分,为了确保我们覆盖每个顶点,我们也可以对每个节点运行 BFS 算法。
BFS 示例
让我们通过一个例子来了解广度优先搜索算法的工作原理。我们使用一个具有 5 个顶点的无向图。
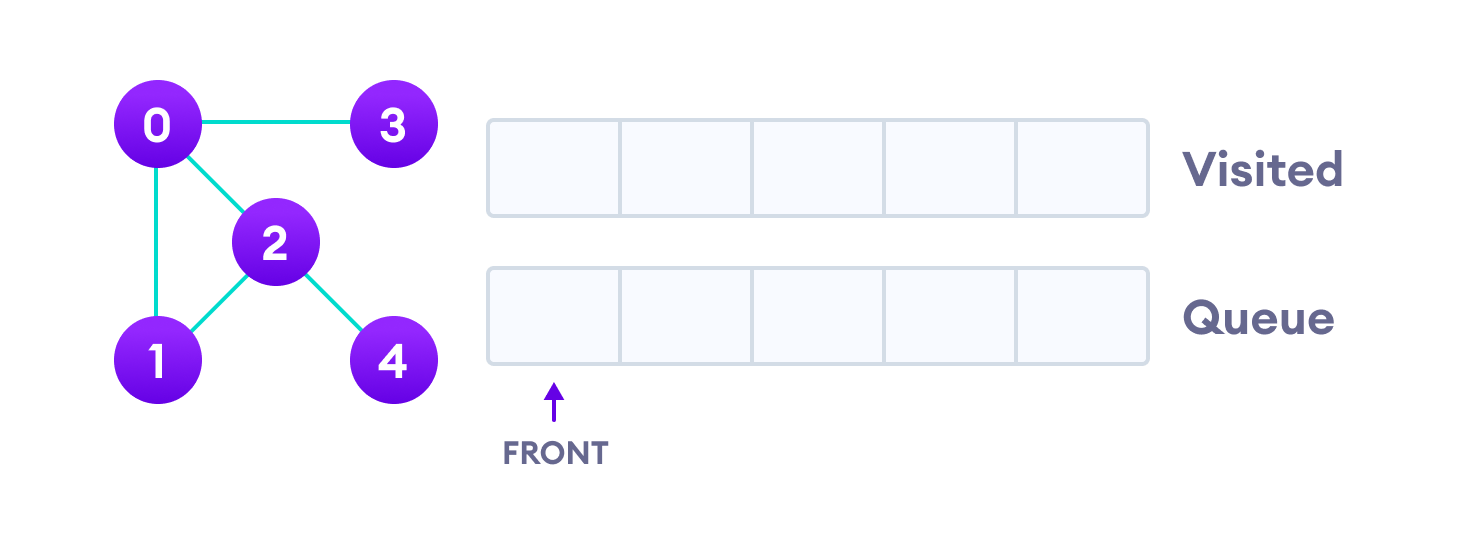
我们从顶点 0 开始,BFS 算法首先将其放入已访问列表,并将其所有邻接顶点放入队列。
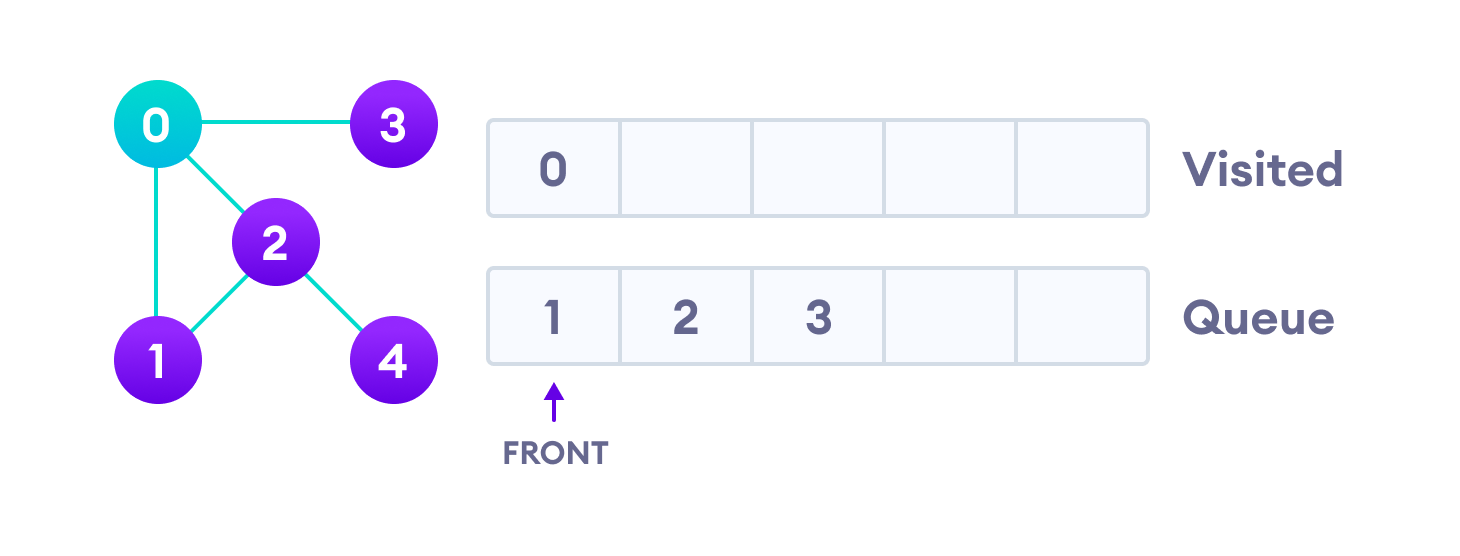
接下来,我们访问队列中的第一个元素,即 1,并转到其邻接节点。由于 0 已被访问,我们转而访问 2。
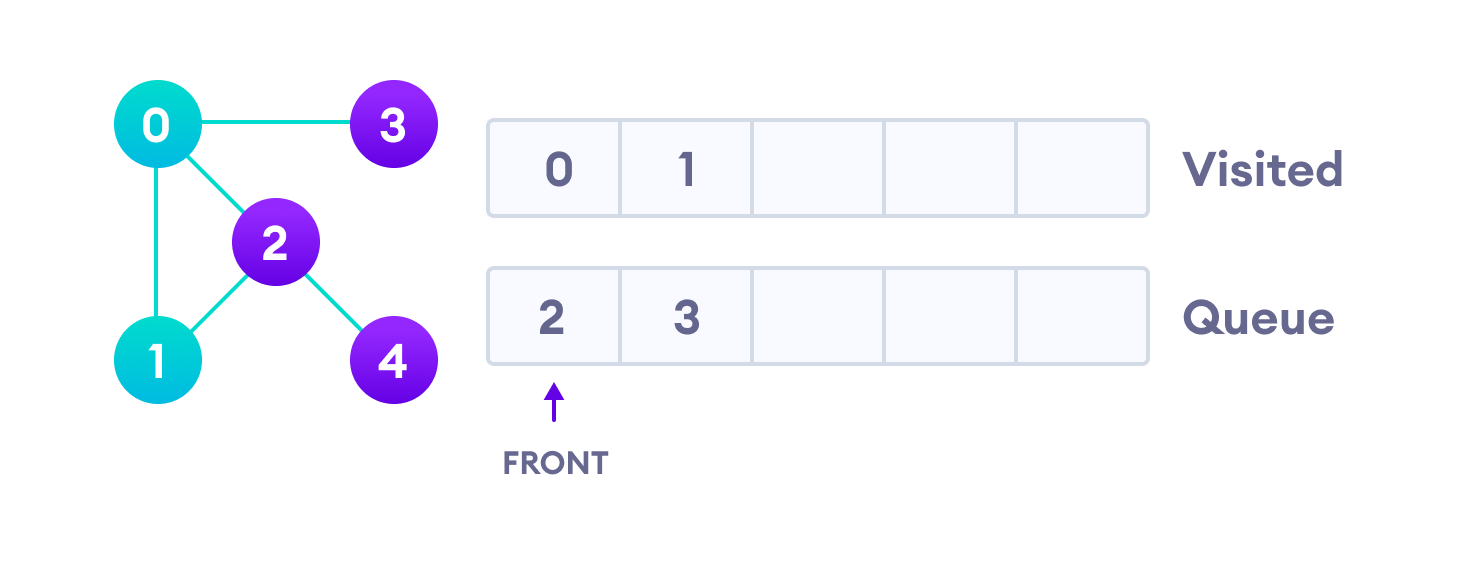
顶点 2 有一个未访问的邻接顶点 4,所以我们将它添加到队列的末尾,并访问队列开头的 3。
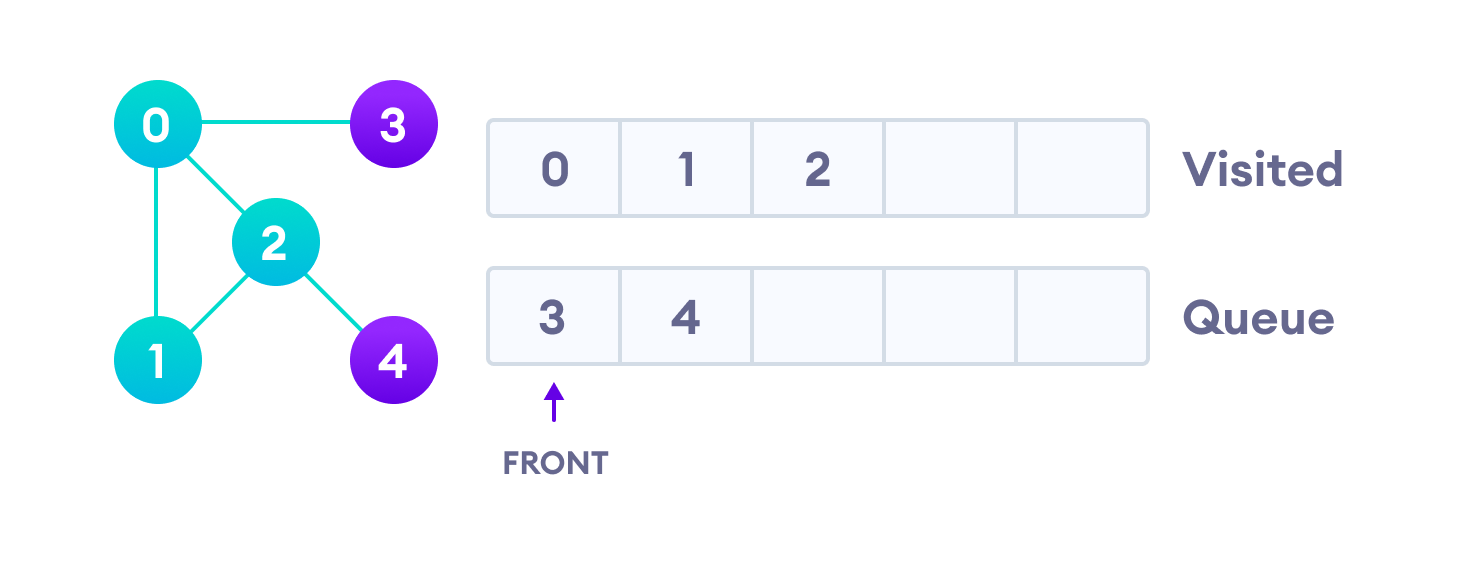
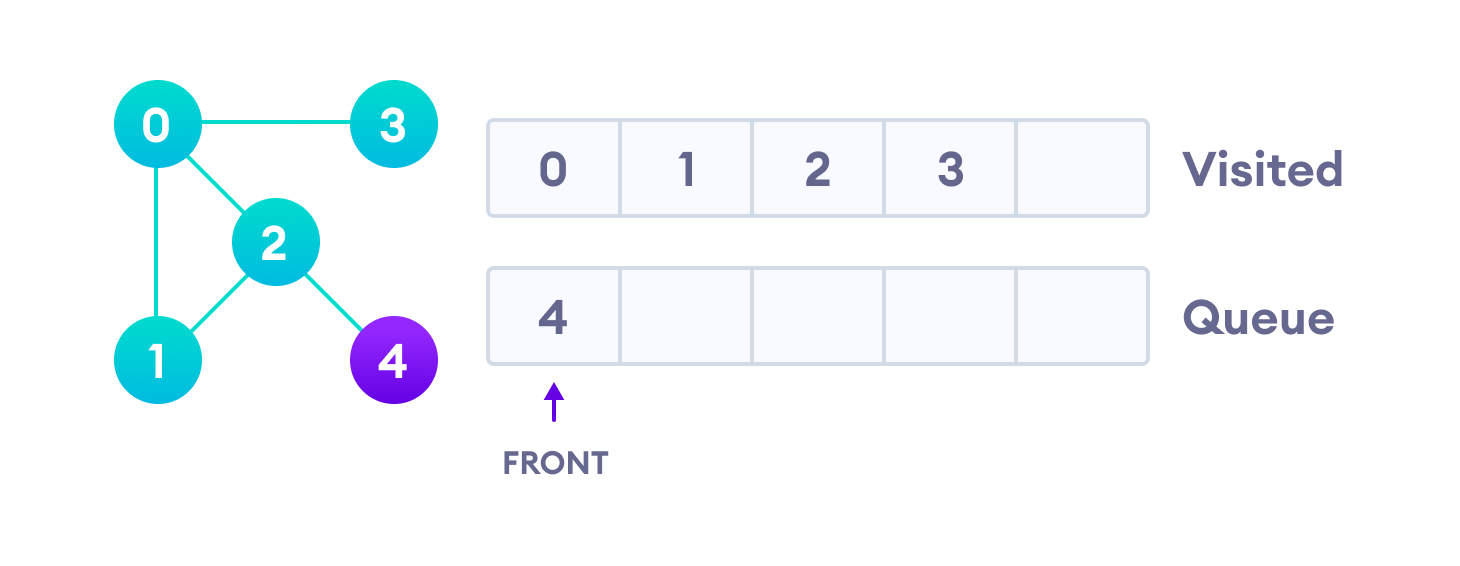
由于 3 的唯一邻接节点 0 已经被访问,队列中只剩下 4。我们访问它。
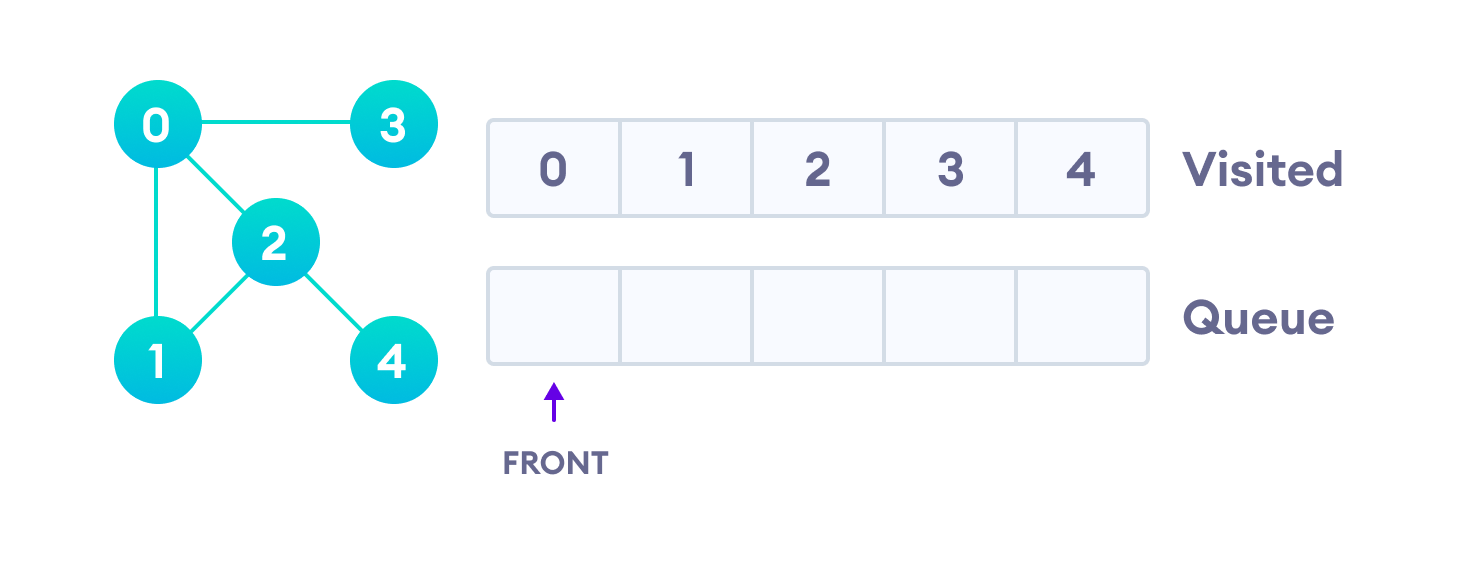
由于队列为空,我们已完成图的广度优先遍历。
BFS 伪代码
create a queue Q
mark v as visited and put v into Q
while Q is non-empty
remove the head u of Q
mark and enqueue all (unvisited) neighbours of u
Python、Java 和 C/C++ 示例
下面显示了带有示例的广度优先搜索算法的代码。代码已简化,以便我们能专注于算法而不是其他细节。
# BFS algorithm in Python
import collections
# BFS algorithm
def bfs(graph, root):
visited, queue = set(), collections.deque([root])
visited.add(root)
while queue:
# Dequeue a vertex from queue
vertex = queue.popleft()
print(str(vertex) + " ", end="")
# If not visited, mark it as visited, and
# enqueue it
for neighbour in graph[vertex]:
if neighbour not in visited:
visited.add(neighbour)
queue.append(neighbour)
if __name__ == '__main__':
graph = {0: [1, 2], 1: [2], 2: [3], 3: [1, 2]}
print("Following is Breadth First Traversal: ")
bfs(graph, 0)
// BFS algorithm in Java
import java.util.*;
public class Graph {
private int V;
private LinkedList<Integer> adj[];
// Create a graph
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList();
}
// Add edges to the graph
void addEdge(int v, int w) {
adj[v].add(w);
}
// BFS algorithm
void BFS(int s) {
boolean visited[] = new boolean[V];
LinkedList<Integer> queue = new LinkedList();
visited[s] = true;
queue.add(s);
while (queue.size() != 0) {
s = queue.poll();
System.out.print(s + " ");
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
}
}
public static void main(String args[]) {
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println("Following is Breadth First Traversal " + "(starting from vertex 2)");
g.BFS(2);
}
}// BFS algorithm in C
#include <stdio.h>
#include <stdlib.h>
#define SIZE 40
struct queue {
int items[SIZE];
int front;
int rear;
};
struct queue* createQueue();
void enqueue(struct queue* q, int);
int dequeue(struct queue* q);
void display(struct queue* q);
int isEmpty(struct queue* q);
void printQueue(struct queue* q);
struct node {
int vertex;
struct node* next;
};
struct node* createNode(int);
struct Graph {
int numVertices;
struct node** adjLists;
int* visited;
};
// BFS algorithm
void bfs(struct Graph* graph, int startVertex) {
struct queue* q = createQueue();
graph->visited[startVertex] = 1;
enqueue(q, startVertex);
while (!isEmpty(q)) {
printQueue(q);
int currentVertex = dequeue(q);
printf("Visited %d\n", currentVertex);
struct node* temp = graph->adjLists[currentVertex];
while (temp) {
int adjVertex = temp->vertex;
if (graph->visited[adjVertex] == 0) {
graph->visited[adjVertex] = 1;
enqueue(q, adjVertex);
}
temp = temp->next;
}
}
}
// Creating a node
struct node* createNode(int v) {
struct node* newNode = malloc(sizeof(struct node));
newNode->vertex = v;
newNode->next = NULL;
return newNode;
}
// Creating a graph
struct Graph* createGraph(int vertices) {
struct Graph* graph = malloc(sizeof(struct Graph));
graph->numVertices = vertices;
graph->adjLists = malloc(vertices * sizeof(struct node*));
graph->visited = malloc(vertices * sizeof(int));
int i;
for (i = 0; i < vertices; i++) {
graph->adjLists[i] = NULL;
graph->visited[i] = 0;
}
return graph;
}
// Add edge
void addEdge(struct Graph* graph, int src, int dest) {
// Add edge from src to dest
struct node* newNode = createNode(dest);
newNode->next = graph->adjLists[src];
graph->adjLists[src] = newNode;
// Add edge from dest to src
newNode = createNode(src);
newNode->next = graph->adjLists[dest];
graph->adjLists[dest] = newNode;
}
// Create a queue
struct queue* createQueue() {
struct queue* q = malloc(sizeof(struct queue));
q->front = -1;
q->rear = -1;
return q;
}
// Check if the queue is empty
int isEmpty(struct queue* q) {
if (q->rear == -1)
return 1;
else
return 0;
}
// Adding elements into queue
void enqueue(struct queue* q, int value) {
if (q->rear == SIZE - 1)
printf("\nQueue is Full!!");
else {
if (q->front == -1)
q->front = 0;
q->rear++;
q->items[q->rear] = value;
}
}
// Removing elements from queue
int dequeue(struct queue* q) {
int item;
if (isEmpty(q)) {
printf("Queue is empty");
item = -1;
} else {
item = q->items[q->front];
q->front++;
if (q->front > q->rear) {
printf("Resetting queue ");
q->front = q->rear = -1;
}
}
return item;
}
// Print the queue
void printQueue(struct queue* q) {
int i = q->front;
if (isEmpty(q)) {
printf("Queue is empty");
} else {
printf("\nQueue contains \n");
for (i = q->front; i < q->rear + 1; i++) {
printf("%d ", q->items[i]);
}
}
}
int main() {
struct Graph* graph = createGraph(6);
addEdge(graph, 0, 1);
addEdge(graph, 0, 2);
addEdge(graph, 1, 2);
addEdge(graph, 1, 4);
addEdge(graph, 1, 3);
addEdge(graph, 2, 4);
addEdge(graph, 3, 4);
bfs(graph, 0);
return 0;
}// BFS algorithm in C++
#include <iostream>
#include <list>
using namespace std;
class Graph {
int numVertices;
list<int>* adjLists;
bool* visited;
public:
Graph(int vertices);
void addEdge(int src, int dest);
void BFS(int startVertex);
};
// Create a graph with given vertices,
// and maintain an adjacency list
Graph::Graph(int vertices) {
numVertices = vertices;
adjLists = new list<int>[vertices];
}
// Add edges to the graph
void Graph::addEdge(int src, int dest) {
adjLists[src].push_back(dest);
adjLists[dest].push_back(src);
}
// BFS algorithm
void Graph::BFS(int startVertex) {
visited = new bool[numVertices];
for (int i = 0; i < numVertices; i++)
visited[i] = false;
list<int> queue;
visited[startVertex] = true;
queue.push_back(startVertex);
list<int>::iterator i;
while (!queue.empty()) {
int currVertex = queue.front();
cout << "Visited " << currVertex << " ";
queue.pop_front();
for (i = adjLists[currVertex].begin(); i != adjLists[currVertex].end(); ++i) {
int adjVertex = *i;
if (!visited[adjVertex]) {
visited[adjVertex] = true;
queue.push_back(adjVertex);
}
}
}
}
int main() {
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
g.BFS(2);
return 0;
}BFS 算法复杂度
BFS 算法的时间复杂度表示为 O(V + E),其中 V 是节点数,E 是边数。
该算法的空间复杂度为 O(V)。
BFS 算法应用
- 通过搜索索引构建索引
- 用于 GPS 导航
- 路径查找算法
- 在 Ford-Fulkerson 算法中查找网络中的最大流
- 在无向图中检测循环
- 在 最小生成树 中
