NumPy 矩阵操作

矩阵是一种二维数据结构，数字排列成行和列。例如，

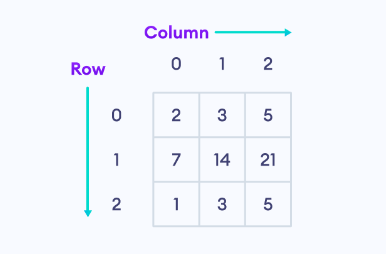
上面的矩阵是一个 **3x3**（读作“三乘三”）矩阵，因为它有 **3** 行和 **3** 列。

NumPy 矩阵操作

以下是 NumPy 提供的一些基本矩阵运算。

在 NumPy 中创建矩阵

在 NumPy 中，我们使用 np.array() 函数来创建矩阵。例如，

import numpy as np

# create a 2x2 matrix
matrix1 = np.array([[1, 3], 
                   [5, 7]])

print("2x2 Matrix:\n",matrix1)

# create a 3x3  matrix
matrix2 = np.array([[2, 3, 5],
             	    [7, 14, 21],
                    [1, 3, 5]])
                    
print("\n3x3 Matrix:\n",matrix2)

输出

2x2 Matrix:
[[1 3]
 [5 7]]

3x3 Matrix:
 [[ 2  3  5]
 [ 7 14 21]
 [ 1  3  5]]

在这里，我们分别通过将列表的列表传递给 np.array() 函数，创建了两个矩阵：一个 **2x2** 矩阵和一个 **3x3** 矩阵。

在 NumPy 中执行矩阵乘法

我们使用 np.dot() 函数来执行两个矩阵之间的乘法。

让我们看一个例子。

import numpy as np

# create two matrices
matrix1 = np.array([[1, 3], 
             		[5, 7]])
             
matrix2 = np.array([[2, 6], 
                    [4, 8]])

# calculate the dot product of the two matrices
result = np.dot(matrix1, matrix2)

print("matrix1 x matrix2: \n",result)

输出

matrix1 x matrix2: 
[[14 30]
 [38 86]]

在此示例中，我们使用 np.dot(matrix1, matrix2) 函数对 matrix1 和 matrix2 这两个矩阵执行矩阵乘法。

要了解更多关于矩阵乘法的信息，请访问NumPy 矩阵乘法。

注意：只有当矩阵具有相同的维度大小时，我们才能进行点积运算。例如，对于 A = (M x N) 和 B = (N x K)，当我们对 C = A . B 进行点积运算时，结果矩阵的大小为 C = (M x K)。

转置 NumPy 矩阵

矩阵的转置是一个通过交换行和列得到的新矩阵。对于 2x2 矩阵，

Matrix:
a11    a12    
a21    a22    

Transposed Matrix:
a11    a21
a12    a22

在 NumPy 中，我们可以使用 np.transpose() 函数获得矩阵的转置。例如，

import numpy as np

# create a matrix
matrix1 = np.array([[1, 3], 
             		[5, 7]])

# get transpose of matrix1
result = np.transpose(matrix1)

print(result)

输出

[[1 5]
 [3 7]]

在这里，我们使用 np.transpose(matrix1) 函数来获得 matrix1 的转置。

注意：或者，我们也可以使用 .T 属性来获取矩阵的转置。例如，如果我们用前面的例子中的 matrix1.T，结果将是相同的。

在 NumPy 中计算矩阵的逆

在 NumPy 中，我们使用 np.linalg.inv() 函数来计算给定矩阵的逆。

然而，需要注意的是，并非所有矩阵都有逆。只有行列式非零的方阵才有逆。

现在，让我们使用 np.linalg.inv() 来计算方阵的逆。

import numpy as np

# create a 3x3 square matrix
matrix1 = np.array([[1, 3, 5], 
             		[7, 9, 2],
                    [4, 6, 8]])

# find inverse of matrix1
result = np.linalg.inv(matrix1)

print(result)

输出

[[-1.11111111 -0.11111111  0.72222222]
 [ 0.88888889  0.22222222 -0.61111111]
 [-0.11111111 -0.11111111  0.22222222]]

注意：如果我们尝试找到非方阵的逆，我们会收到一条错误消息：numpy.linalg.linalgerror: Last 2 dimensions of the array must be square（数组的最后两个维度必须是方的）。

在 NumPy 中查找矩阵的行列式

我们可以使用 np.linalg.det() 函数来查找方阵的行列式，以计算给定矩阵的行列式。

假设我们有一个 **2x2** 矩阵 A

a b
c d

所以，一个 **2x2** 矩阵的行列式将是

det(A) = ad - bc

其中 **a, b, c** 和 **d** 是矩阵的元素。

让我们看一个例子。

import numpy as np

# create a matrix
matrix1 = np.array([[1, 2, 3], 
             		[4, 5, 1],
                    [2, 3, 4]])

# find determinant of matrix1
result = np.linalg.det(matrix1)

print(result)

输出

-5.00

在这里，我们使用 np.linalg.det(matrix1) 函数来查找方阵 matrix1 的行列式。

展平 NumPy 矩阵

展平矩阵只是将矩阵转换为一维数组。

要将矩阵展平为一维数组，我们使用 array.flatten() 函数。让我们看一个例子。

import numpy as np

# create a 2x3 matrix
matrix1 = np.array([[1, 2, 3], 
             		[4, 5, 7]])

result = matrix1.flatten()
print("Flattened 2x3 matrix:", result)

输出

Flattened 2x3 matrix: [1 2 3 4 5 7]

在这里，我们使用 matrix1.flatten() 函数将 matrix1 展平成一维数组，而不会丢失其任何元素。