相关性是一个统计概念,它量化了两个变量相互关联的程度。
在 Pandas 中,可以使用 corr() 函数计算相关性。
让我们看一个例子。
import pandas as pd
# create dataframe
data = {
"Temperature": [22, 25, 32, 28, 30],
"Ice_Cream_Sales": [105, 120, 135, 130, 125]
}
df = pd.DataFrame(data)
# calculate correlation matrix
print(df.corr())输出
Temperature Ice_Cream_Sales Temperature 1.000000 0.923401 Ice_Cream_Sales 0.923401 1.000000
在本例中,我们在 DataFrame df 上使用了 corr() 方法来计算列之间的相关系数。
输出是一个相关矩阵,显示了 DataFrame 中所有列对之间的相关系数。在本例中,只有两列,所以矩阵是2x2。
在这里,Temperature 和 Ice_Cream_Sales 之间的相关系数为0.923401,这是一个正值。这表明随着温度的升高,冰淇淋的销量也随之增加。
对角线上的系数值为1.000000,表示每列与其自身的关联度。
正相关和负相关
正相关是指两个变量之间的一种关系,它们都倾向于朝着同一方向变化。当一个变量增加时,另一个变量也倾向于增加;当一个变量减少时,另一个变量也倾向于减少。
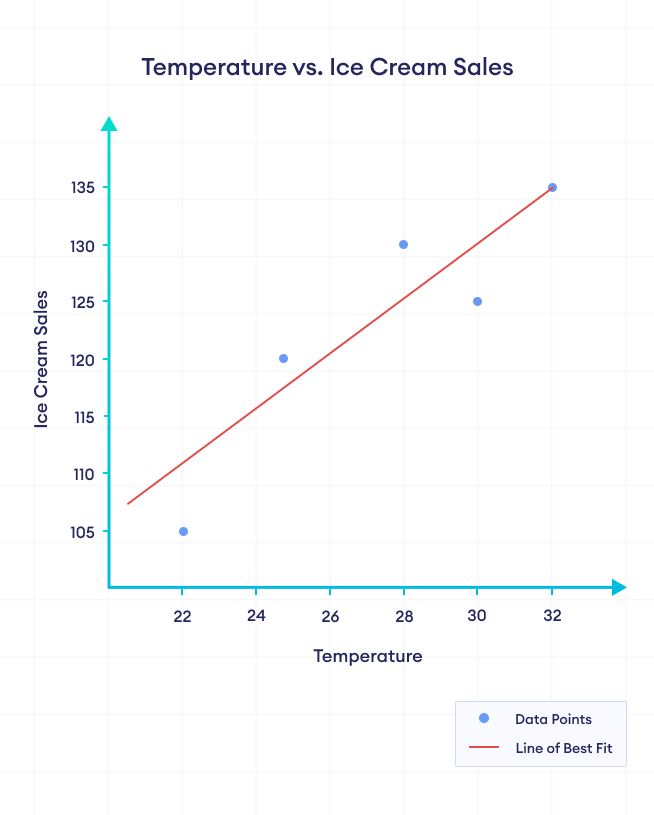
在上图中,我们可以清楚地看到,随着温度的升高,冰淇淋的销量也在增加。我们可以说温度和冰淇淋销量之间存在正相关。
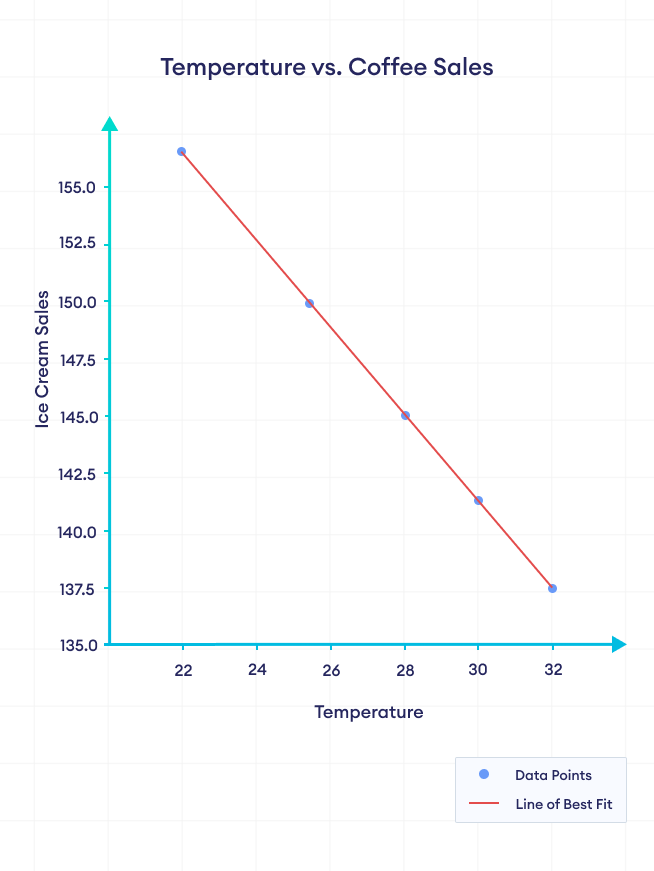
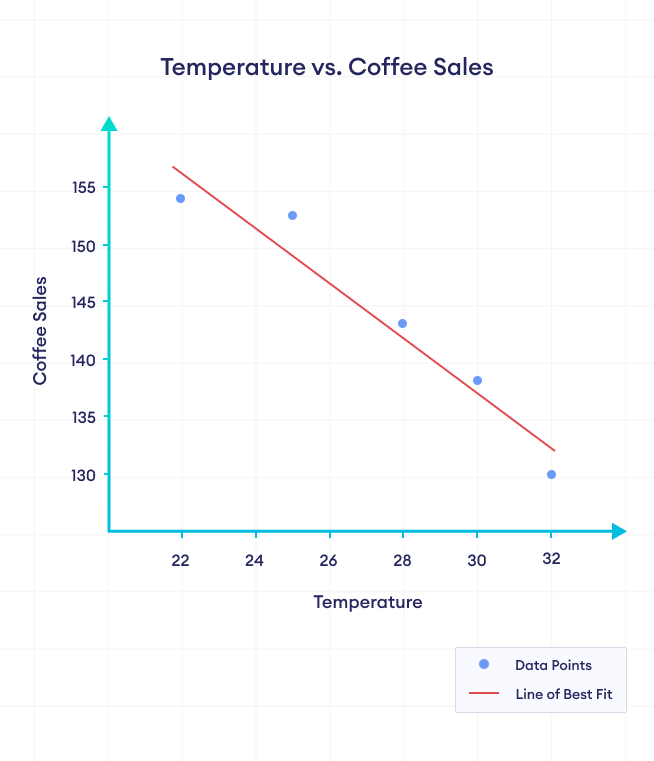
另一方面,负相关是指两个变量之间的一种关系,它们倾向于朝着相反的方向变化。当一个变量增加时,另一个变量倾向于减少,反之亦然。
在上图中,随着温度的升高,咖啡的销量在下降。我们可以说温度和咖啡销量之间存在负相关。
示例:两列之间的相关性
我们可以指定要计算相关性的列,而不是查找整个相关矩阵。
import pandas as pd
# create dataframe
data = {
"Temperature": [22, 25, 32, 28, 30],
"Ice_Cream_Sales": [105, 120, 135, 130, 125]
}
df = pd.DataFrame(data)
# calculate correlation coefficient
correlation = df['Temperature'].corr(df["Ice_Cream_Sales"])
print(correlation)输出
0.9234007664064656
在本例中,我们计算了 Temperature 和 Ice_Cream_Sales 之间的相关性。
执行此操作的语法是
df['column1'].corr(df['column2'])示例:缺失值
DataFrame 可能包含缺失值(NaN)。corr() 函数会完全忽略包含 NaN 值的行。
import pandas as pd
import numpy as np
# create a dataframe
data = {
"Temperature": [22, 25, 32, 28, 30],
"Coffee_Sales": [158, 145, np.nan, np.nan, 140]
}
df = pd.DataFrame(data)
# calculate correlation between Temperature and Ice_Cream_sales
correlation1 = df["Temperature"].corr(df["Coffee_Sales"])
print("With NaN values")
print(df)
print(f"correlation = {correlation1}")
print()
# remove missing values
df.dropna(inplace=True)
# calculate correlation between Temperature and Ice_Cream_sales
correlation2 = df["Temperature"].corr(df["Coffee_Sales"])
print("Without NaN values")
print(df)
print(f"correlation = {correlation2}")
print()输出
With NaN values Temperature Coffee_Sales 0 22 158.0 1 25 145.0 2 32 NaN 3 28 NaN 4 30 140.0 correlation = -0.923177938058926 Without NaN values Temperature Coffee_Sales 0 22 158.0 1 25 145.0 4 30 140.0 correlation = -0.923177938058926
请注意,相关值在删除 NaN 值之前和之后是相同的。这意味着 corr() 会完全忽略 NaN 值。
我们使用了 NumPy 库来生成 NaN 值。
Pandas 中的相关性方法
我们可以使用 Pandas 中的三种不同方法来计算相关性
- Pearson 方法(默认):评估两个连续变量之间的线性关系
- Kendall 方法:衡量两个测量量之间的序数关联
- Spearman 方法:评估两个连续变量或有序变量之间的单调关系
默认情况下,corr() 计算 Pearson 相关系数,它衡量两个变量之间的线性关系。
示例:Pearson、Kendall 和 Spearman 方法
import pandas as pd
# create dataframe
data = {
"Temperature": [22, 25, 32, 28, 30],
"Ice_Cream_Sales": [105, 120, 135, 130, 125]
}
df = pd.DataFrame(data)
# calculate different correlation coefficients
pearson = df['Temperature'].corr(df["Ice_Cream_Sales"])
kendall = df['Temperature'].corr(df["Ice_Cream_Sales"], method='kendall')
spearman = df['Temperature'].corr(df["Ice_Cream_Sales"], method='spearman')
# display different correlation coefficient
print(f"Pearson's Coefficient: {pearson}")
print(f"Kendall's Coefficient: {kendall}")
print(f"Spearman's Coefficient: {spearman}")输出
Pearson's Coefficient: 0.9234007664064656 Kendall's Coefficient: 0.7999999999999999 Spearman's Coefficient: 0.8999999999999998
在此,Pearson 系数的数值最高,这表明相关性主要是线性的。
完美、良好和差的相关性
我们可以将相关值解释为
完美相关
完美的正相关意味着,一个变量的每一次增加,另一个变量都会相应地增加,以系数 +1 表示。
完美的负相关,用 -1 表示,意味着一个变量的增加会导致另一个变量成比例地减少。
良好的相关性
良好的相关性范围可以从 0.5 到 0.9(正或负),通常表示变量之间存在很强的关系,但并不意味着关系是完美的。
差的相关性
差的相关性通常接近于零,这表明两个变量之间没有关系或任何形式的依赖关系。