二进制数与计算机的运作

虽然掌握渊博的数学知识对于学习计算机编程并非必需，但对构成计算基础的一些基本数学概念有所了解，无疑会有很大帮助。而还有什么能比二进制数学更基础地构成现代计算的基石呢？

“二进制”这个词意味着某物只有两种可能的对象或状态。在二进制数制中，这两种对象就是数字 0 和 1。这两个数字可以代表各种事物。

例如，在计算机逻辑中，0 代表“假”，而 1 代表“真”。或者，它们可以作为 1 和 0 的组合来表示普通数字。例如，用三个二进制数字表示 0、1、2、3 和 4 分别是 000、001、010、011 和 100。

但从计算的基本层面来看，这一切意味着什么？为什么二进制数制被用作我们所有计算的基础？

也许如果我们能理解计算机在机器层面的基本运作方式，就更容易理解这一切。

0 和 1：解读计算机电路的运作

计算机依靠这些电路产生的电信号进行运算。为了设计出运行高效的计算机，我们需要一种能够以简化且有效的方式解释电信号的系统。

一种很好的方法是将电信号解释为二进制值：0 代表低电压值，1 代表高电压值。一个更简单的思考方式是想象一个灯泡。如果灯泡是熄灭的，那么这个状态就被解释为具有值 0。如果它是亮着的，那么它就被解释为具有值 1。

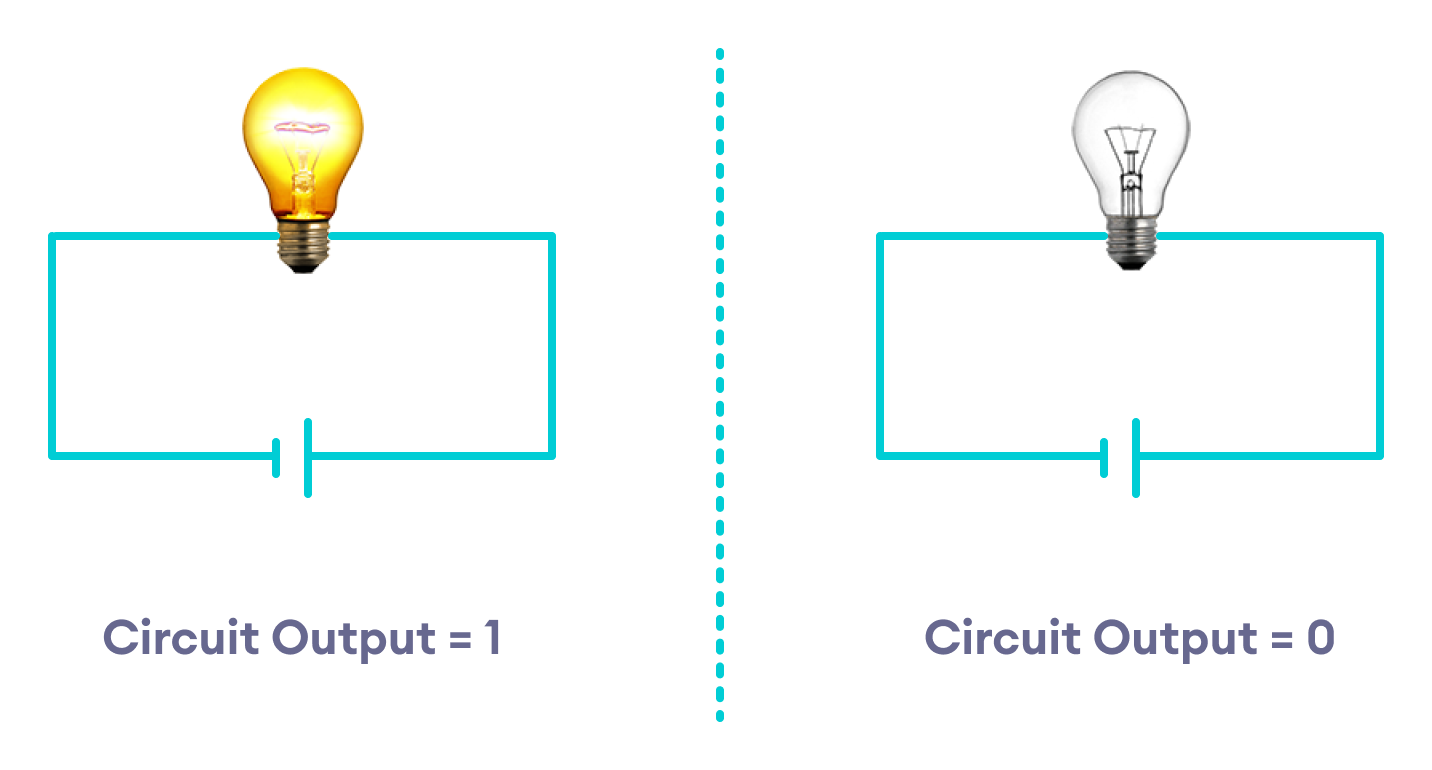
这种广泛的概括将每个电信号的解释范围缩小到两个明确的值，而不是一个无限范围的连续电压值。

有了这种处理和解释电子电路的方法，我们就可以基于二进制位设计编码系统，以辅助我们的计算任务。这些系统可以是二进制逻辑（仅限于真或假值）、数值的基数为 2 的表示法，或者使用依赖于一系列二进制数来表示文本、图像或声音的其他系统。

本质上，我们的计算机使用一系列高电压和低电压的电信号（二进制值）来表示从文本和数字到图像和声音的一切。有特殊的电子电路，如触发器和其他电路，它们可以“存储”或保留这些特定的电信号模式以供延长使用。

例如，一个触发器可能有多个输入，当前输出为高电压（我们解释为 1）。假设接下来的两个触发器输出为低电压 0。我们可以将这三个输出组合起来得到值 100，这在二进制中等于数字 4。

因此，理解二进制数可以帮助我们足够抽象地理解计算机运算的一些基本原理，即使我们微弱的人类智力可能永远无法理解计算机运算的全部复杂性。

这也很不错，因为对于我们计算机科学的学生来说，处理简化的和抽象的计算机运算概念已经绰绰有余。在接下来的章节中，我们将简要探讨计算机使用二进制符号执行一些最基本运算的一些方式。

布尔逻辑：使用二进制数理解计算机逻辑

计算机程序使用一种非常特定的逻辑系统来执行其指令。这被称为布尔逻辑，由 19 世纪英国数学家乔治·布尔创立。

布尔创立了一个算术和逻辑运算系统，该系统利用二进制数制。布尔逻辑只处理两个可能的值：真或假。真用 1 表示，假用 0 表示。所有逻辑运算的结果都只产生这两个二进制值之一。

现代计算机一直使用这种形式的逻辑来做决策。这些决策导致我们的计算机采取特定行动而不是另一种。

要认识到这个系统对计算机有多么关键，我们只需看看大多数编程语言中的逻辑运算符：AND、OR 和 NOT 运算符。

这些运算符直接取自布尔逻辑的 AND、OR 和 NOT 运算。任何对编程有初步了解的人都知道，这些运算是编程的核心。

但布尔工作的影响不止于此。事实上，许多编程语言都有一个名为 boolean 的数据类型，它只能存储“真”或“假”，即 1 或 0。

这些布尔变量和逻辑运算符是实现编程语言中的条件语句和控制语句的基本组成部分。因此，它们的重要性怎么强调都不为过，因为这是编程入门（Programming 101）。

我们还可以在编程语言中使用二进制数进行许多其他更有创意、更复杂的方式。然而，这篇博文仅是对二进制数可以用于的某些方面的概述。

因此，我们不会深入探讨任何技术编程细节。也许我会在以后的博文中探讨更多这些主题。目前，让我们只探索数值表示这个更简单的主题。

基数为 2 的数值表示

我们的计算机系统以某种形式的基数为 2 的数制来表示数值。我们日常生活中使用的普通数字是基数为 10 的数制。例如，数字 135 代表一百三十五。

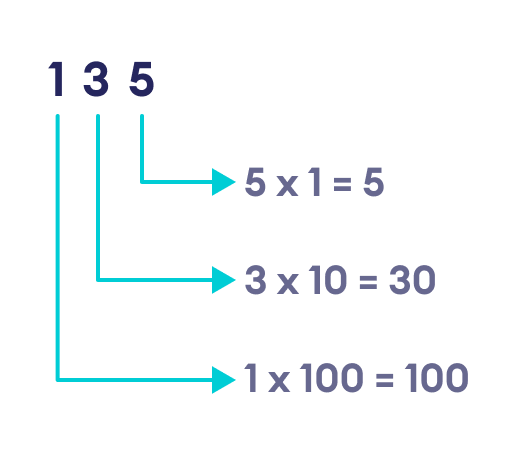
从上图可以看出，从右侧开始的每一位数字都乘以 10 的递增幂，从 (10 ^ 0 = 1) 开始，然后是 (10 ^ 1 = 10)，最后是 (10 ^ 2 = 100)。数字越多，10 的幂的序列就越长。这就是为什么这个数制被称为基数为 10 的数制。

基数为 2 的数制的工作方式相同，只是我们将每一位（二进制“数字”）乘以 2 的连续幂。例如，让我们取基数为 2 的数字 1011，看看它代表哪个基数为 10 的数字。

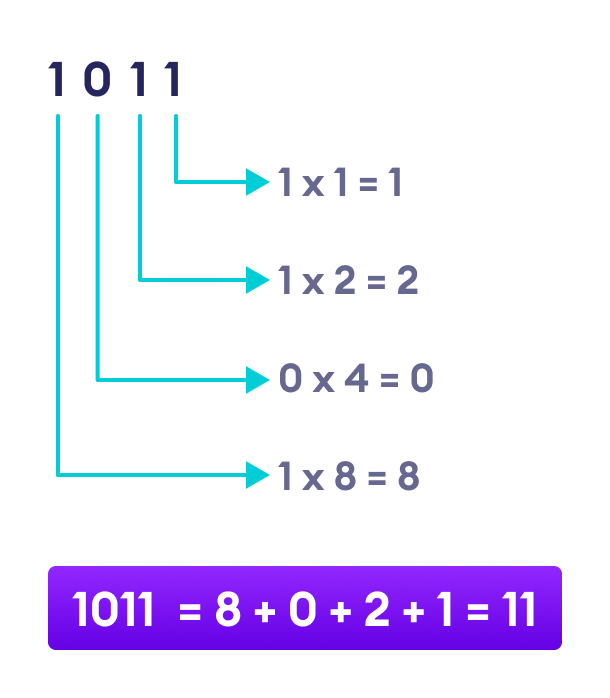
正如我们所见，二进制数 1011 在基数为 10 的情况下等同于数字 11。

当然，二进制数的组合方式也很重要。我们知道 1011 在基数为 10 的情况下代表数字 11。但是如果我们把相同的一系列位组合成 10 11 呢？它们是两个不同的数字 10 和 11 吗？或者它们是单个数字 1011 吗？

这向我们展示了我们组合数字方式的重要性。在计算机中，数字以多种不同的方式组合。例如，C++ 中的整数数据类型 int 将单个数字存储在一系列 32 个二进制数中。所以，基数为 10 的数字 0 由一系列 32 个零表示，而数字 1 由左侧有 31 个零的前导 1 表示。

文本和字符表示

我们已经看到，基数为 2 的数制是我们电子设备中数值表示的基础。虽然这对于文本表示系统来说是真的，但它们的工作方式却大不相同。

表示字符最常见的系统是 ASCII（美国信息交换标准代码）和 Unicode（ASCII 的扩展）。这些系统为字符分配唯一的数值，并以二进制格式存储它们。

例如，ASCII 系统最初使用 7 位来表示一个字符。目前已扩展到 8 位。例如，字符 A 在 ASCII 中由数值 65 表示。65 的二进制是 1000001。请注意，二进制表示包含 7 位。在扩展 ASCII 中，它将存储为 01000001，使总位数达到 8 位。

同样，字符 a 的 ASCII 码是 97，在扩展 ASCII 中用 01100001 表示。还有一些非常特殊的字符由 0、1、2 等表示。它们分别表示为 00000000、00000001、00000010 等。

这个系统对于表示英语和某些欧洲字符和符号来说效果很好，但对于表示世界各地语言的符号来说则远远不够。为了容纳更多的符号，Unicode 应运而生。

Unicode 最初每个符号使用 21 位，而 ASCII 最初使用 7 位。这大大扩展了可以用来表示字符的值的范围。原始的 ASCII 码包含在 Unicode 系统中。

目前，基于 Unicode 的编码系统，称为 UTF-8，是 Web 应用程序中最常用的编码系统。UTF-8 每个符号最多可以使用 32 位，这意味着它可以表示更多种类的字符。

像素和图像

毫不奇怪，图像也经常用数字表示。在计算机中，图像最常由称为像素的微小彩色方块构成。想象一下现实生活中的马赛克：图像或图案是通过将许多小的彩色碎片组合在一起形成的。或者像拼图一样，我们将小块组合起来创造一个更大、完整的图像。

像素的工作方式类似。成千上万个微小的彩色方块构成了显示在我们屏幕上的图像。像素中的颜色有许多编码方式，但最常用的代码是 RGB 代码（红、绿、蓝）。

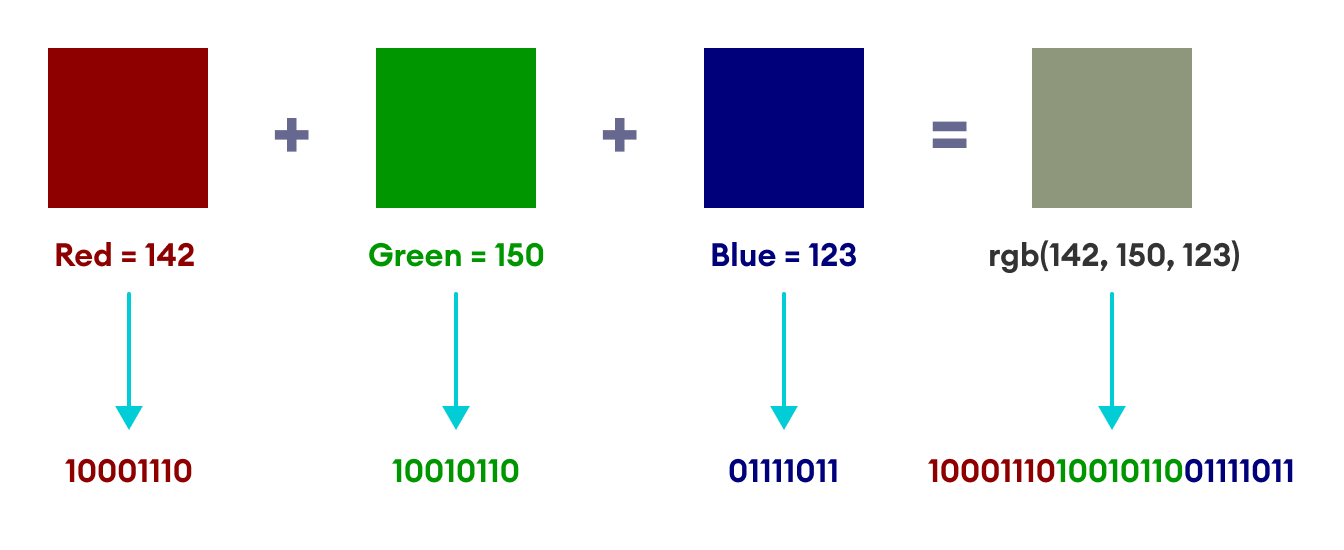
RGB 代码通过组合红色、绿色和蓝色来产生我们在现代设备中看到的所有色调。三个颜色分量中的每一个都由一个数字编码，其值范围从 0 到 255。因此，有三组数字来描述一个像素。

例如，让我们考虑由 RGB 代码 (142, 150, 123) 表示的颜色。此颜色代码有 3 个分量：红 = 142，绿 = 150，蓝 = 123。

在我们计算机内部，每个颜色分量都用 8 位二进制等价物表示，然后将它们组合在一起。例如，142（红色分量）的二进制是 10001110，150 的二进制是 10010110，123 的二进制是 01111011。

红 = 142 = 10001110

绿 = 150 = 10010110

蓝 = 123 = 01111011

计算机从左到右组合这些数字来在其内存中存储 RGB 代码。

完整的 RGB 代码 = 100011101001011001111011

因此，我们可以看到，即使是图像也用二进制表示。事实上，了解图像像素的二进制代码为有趣的图像操作打开了大门，例如将一张图像隐藏在另一张图像中。我已经在我的上一篇博文《隐写术：在图片中隐藏信息》中写过一种简单的图像隐藏方法。您可以查阅它，了解二进制数在计算机科学中的实际应用。

最后的思考和收获

二进制数构成了现代计算的核心基础之一。虽然我们简要回顾了计算机使用二进制数的一些方式，但我们还遗漏了很多，因为详尽的应用列表和解释超出了这篇博文的范围。

尽管如此，我们在这里已经涵盖了一些有趣的主题，尽管它们可能很基础。我们已经看到：

• 计算机电路的物理活动是通过二进制记法来解释的，即在单个电路上，低电压值被解释为 0，高电压值被解释为 1。
• 计算机在执行逻辑运算时，通过将 1 解释为 真，将 0 解释为 假 来使用布尔逻辑。
• 数字以基数 2 的格式表示，根据应用的不同，以不同数量的位组合（一些数字由 16 位表示，一些由 32 位表示，还有一些由 64 位表示）。
• 字符和文本被分配了唯一的数值，然后将其转换为基数 2 的格式，以 7 位或 8 位 (ASCII) 或 32 位 (UTF-8) 为单位。
• 图像由称为像素的微小彩色方块组成，每个像素都用数字编码，这些数字最终被转换为二进制。

至此，这篇博文就结束了，我希望我已经阐明了二进制数为何对计算如此重要。