秘密和阴谋不必局限于詹姆斯·邦德或杰森·伯恩系列等炫目的间谍电影和小说;使用二进制数,你可以将信息隐藏在一张小的、简单的图片中。
二进制数由0和1组成,它们是被称为二进制数系统或基数为2的数系统的一部分。我们常用的数系统被称为十进制数系统或基数为10的数。
我敢肯定,阅读这篇博文的任何人都熟悉数系统,因为它们是计算的基本组成部分。它们也是隐藏信息在图片中的过程的基本组成部分。
当然,我并不是说我是这个领域的专家;事实上,离那还远着呢。称我为该领域的菜鸟是对真实存在的菜鸟的一种不公正,但我可以说,我了解一个简单算法背后的基本原理。
探索这个算法也许能给你提供动力,让你进一步追求这个领域的复杂性(正如我打算自己做的那样)。如果我们选择这样做,我们在这方面的二进制知识和经验也会随之增加,这对于在编程语言中发挥创意会很有用。
但在深入研究这个激动人心的领域之前,我首先要归功于最初启发这篇博文创作的来源。
我们将要讨论的算法基于伦敦大学金史密斯学院在Coursera在线学习平台提供的出色在线课程。该课程名为“计算机科学数学”,您可以在此处找到其链接:
https://www.coursera.org/learn/mathematics-for-computer-science/
步骤1:理解像素和图像
在开始编写带有秘密消息的图像代码的勇敢的探索之前,我们首先需要理解图像在计算机中是如何表示的。而这一切都始于“像素”。
像素可以被认为是构成图像的最小单位。它本质上是一个小的彩色方块,与其他彩色方块(即其他像素)结合起来以完成图像。
将每个像素想象成一幅大型拼图游戏的一块,将它们组合在一起就能生成一张图像。当然,如果像素只是随意组合,没有任何预先的考虑或计划,那么最终结果很可能是一团混乱的视觉垃圾(也称为“现代艺术”)。
撇开低俗的笑话和对艺术表达的攻击不谈,像素重要的在于它们是由数字表示的。这些数字可以是RGB代码(红、绿、蓝)、十六进制代码、HSL(色相、饱和度、亮度)或其他代码的形式。
以RGB颜色代码为例。在这个配色方案中,我们将红色、绿色和蓝色结合起来,形成我们在设备上看到的所有不同的颜色。
红、绿、蓝的每个单独颜色值范围从0到255。例如,要在我们的屏幕上打印出纯红色,我们使用RGB值rgb(255, 0, 0)。
这里,
- 红色值=255(即红色对像素的最大可能贡献)
- 绿色值=0(即绿色对像素的最小可能贡献)
- 蓝色值=0(即蓝色对像素的最小可能贡献)
同样,要打印出纯绿色,我们使用代码rgb(0, 255, 0),要打印出纯蓝色,我们使用rgb(0, 0, 255)。
要打印黑色,我们将红、绿、蓝的值全部设为0(因为黑色实际上是其他颜色的缺失)。
要打印白色,我们将RGB值全部设为255(因为白色是所有颜色的组合)。
RGB的中间值用于产生我们眼睛可以看到的几乎所有色调的颜色。
至于十六进制代码,它们可以通过将RGB代码转换为十六进制数系统来获得。
这里的要点是颜色由数字表示。这些数字——就像我们知道的所有数字一样——可以转换为二进制。隐藏消息在图像中通常涉及操作这些二进制数的最低有效位。
现在让我们继续下一步:创建一个4x4(16像素)的简单图像,并修改它以隐藏其中的随机数。
步骤2a:在图像中隐藏随机数
让我们考虑下面一个非常简单、基本的图像。
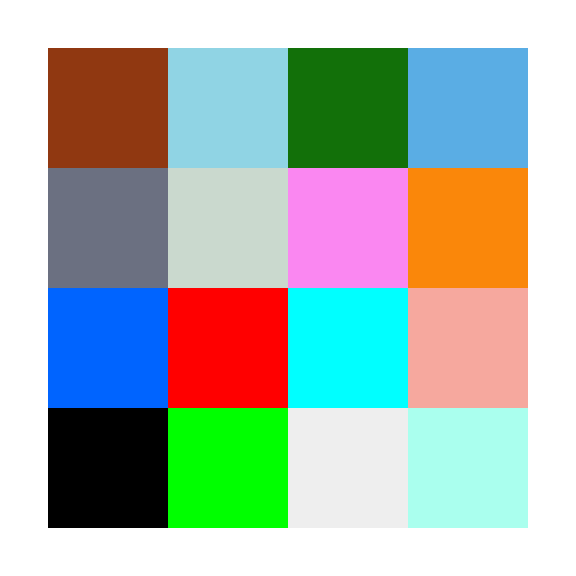
这张图像由16个不同颜色和色调的像素组成,排列成4x4的格式,即它有4行和4列。
我们将隐藏只能用3个二进制数字表示的数字,即0-7的数字。
[注意:二进制数字更常被称为“位”]
你可能会问,为什么只用3位?因为RGB代码只允许3个不同的数字(红色、绿色和蓝色)。我们将隐藏数字的每个二进制位隐藏在每个RGB值的最低有效位中。
为了更清楚起见,我们举个例子。假设我们要将数字“6”隐藏在图像的第一个像素中。第一个像素的RGB代码是rgb(144, 56, 17)。
我们首先将RGB值转换为二进制。所以,
| 颜色 | 十进制系统中的值 | 8位二进制系统中的值 |
| 红色 | 144 | 1001 0000 |
| 绿色 | 56 | 0011 1000 |
| 蓝色 | 17 | 0001 0001 |
数字“6”(我们要隐藏的数字)的二进制等价物是110。我们将110的最左边一位(即1)隐藏在红色二进制值的最右边一位中。
所以,
红色=1001 0001(原为1001 0000)=145
同样,中间的位(即另一个1)隐藏在绿色二进制值的最右边一位中。
即绿色=0011 1001(原为0011 1000)=57
最后,110的最右边一位(即0)隐藏在蓝色二进制值的最右边一位中。
即蓝色=0001 0000(原为0001 0001)=16
这导致我们的编码像素为rgb(145, 57, 16)。
让我们比较一下这两个像素:原始像素(无编码数字)和修改后的像素(编码了数字“6”)。

正如我们所见,这两个像素非常相似,普通眼睛很难分辨出它们之间的区别。
我们对剩余的15个像素重复相同的过程,最终结果是修改后的图像,从普通眼睛看来几乎与原图相同。

这两张图像看起来几乎相同。然而,我们知道由于每个像素的RGB代码的细微修改,它们之间存在细微的差别。
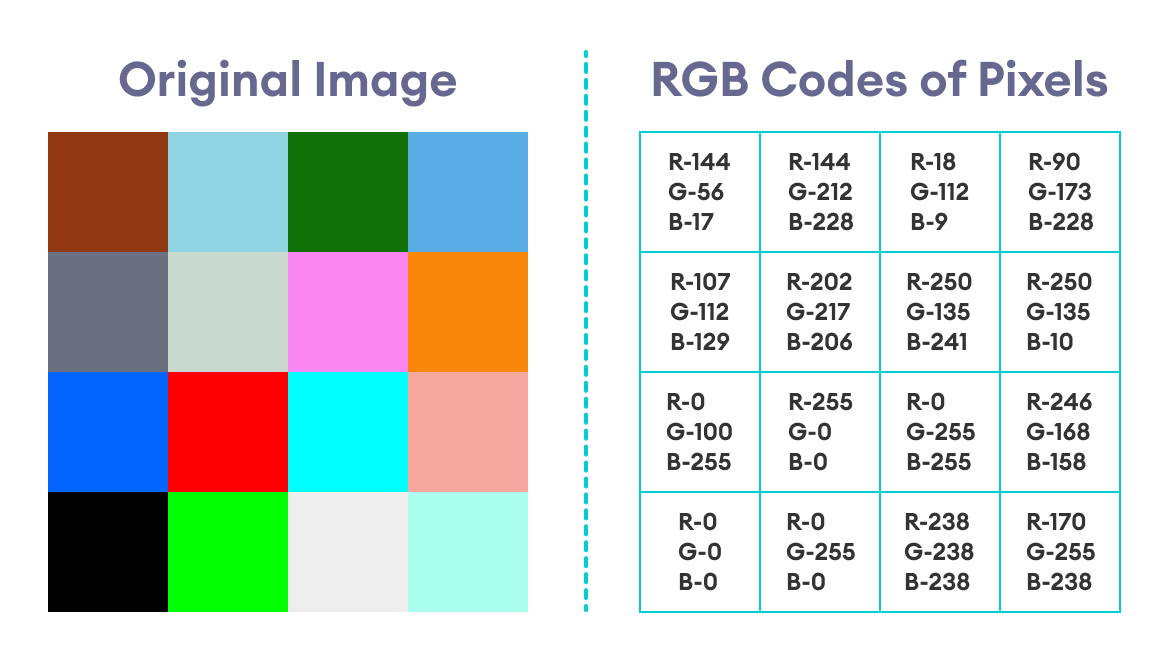
下图显示了原始图像以及每个像素的RGB值。
步骤2b:解码编码图像
为了检索隐藏在我们编码图像中的消息,我们只需反转导致其被编码的过程,即:
- 检索每个像素的RGB代码。
- 取每个RGB代码的红色、绿色和蓝色值的二进制等价物。
- 选择红色、绿色和蓝色二进制值的最右边一位,并将它们组合起来。
- 将生成的二进制数转换为其对应的十进制数。
下图显示了编码图像及其每个像素的相应RGB值。
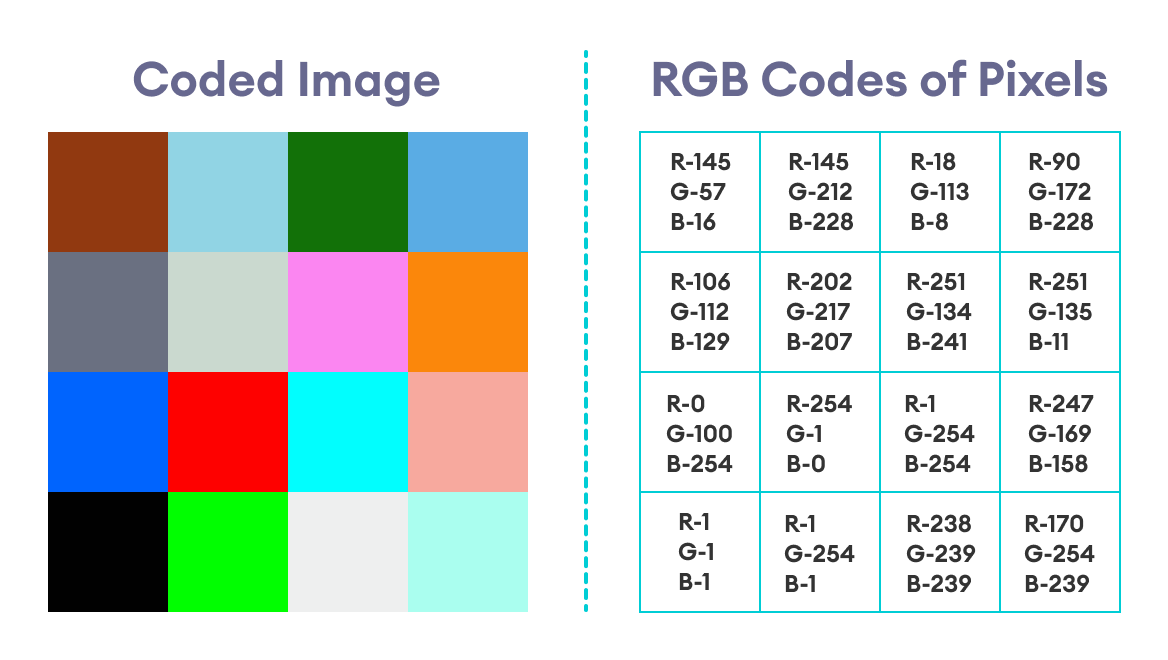
解码图像将为我们提供数字。
6420135702467531
注意:如果我们仔细检查上图和这个简单的算法,我们可以清楚地看到,如果RGB代码的某个分量是偶数,那么该数字就对应于二进制数0,而奇数则对应于二进制数1。
为了进一步阐明这一点,让我们看两个随机像素的RGB代码,比如第1行第3列的像素(我们称之为R1C3)和第3行第4列的像素(R3C4)。
对于像素R1C3,
红色=18(偶数)----> 0
绿色=113(奇数)----> 1
蓝色=8(偶数)----> 0
将这些数字从红到蓝组合起来,我们得到010,这是数字2的二进制代码。
当我们检查秘密消息时,我们会发现在同一位置由该像素表示的数字是2(请参阅上面的秘密消息或下方最终解决方案的图像)。
同样,对于像素R3C4,
红色=247(奇数)----> 1
绿色=169(奇数)----> 1
蓝色=158(偶数)----> 0
将这些数字从红到蓝组合起来,我们得到110,这是数字6的二进制代码。这确实是正确的解决方案。
这个见解很重要,因为它大大缩短了解码图像所需的时间,因为这意味着我们不需要将RGB代码转换为二进制。相反,我们只看数字是偶数还是奇数,并相应地分配值。然后我们将最终解码的二进制数转换为十进制。
因此,每像素需要4次总数转换(3次十进制到二进制用于红、绿、蓝;1次二进制到十进制用于最终解码的二进制消息),而我们只需要进行1次数转换(十进制到二进制)/像素。
秘密消息(及其包含的像素)由下表表示。

需要注意的是,我并没有打算让这里使用的秘密数字代表任何连贯的消息。它们仅仅是随机数字,仅用作示例。
然而,让我强调一下,我将这个例子直接改编自我之前引用的Coursera课程(由伦敦大学和金史密斯学院提供)。
实际上,如果使用讲师那里使用的代码表,这些数字可以代表字母和字符的秘密表示。然而,在我们的例子中,上述消息仅仅是一串随机数字。
所以我强烈建议您访问并探索该在线课程以获得更好的见解。
步骤3a:将一张图像隐藏在另一张图像中
我们可以将我们编码的恶作剧进一步发展,实际上将一张图像隐藏在另一张图像中。在这种情况下,我们操作RGB数字的最后4位二进制数来隐藏图像的颜色代码。
让我们使用我们示例中用于隐藏消息的初始图像。和以前一样,下图显示了图像及其相应的RGB代码。
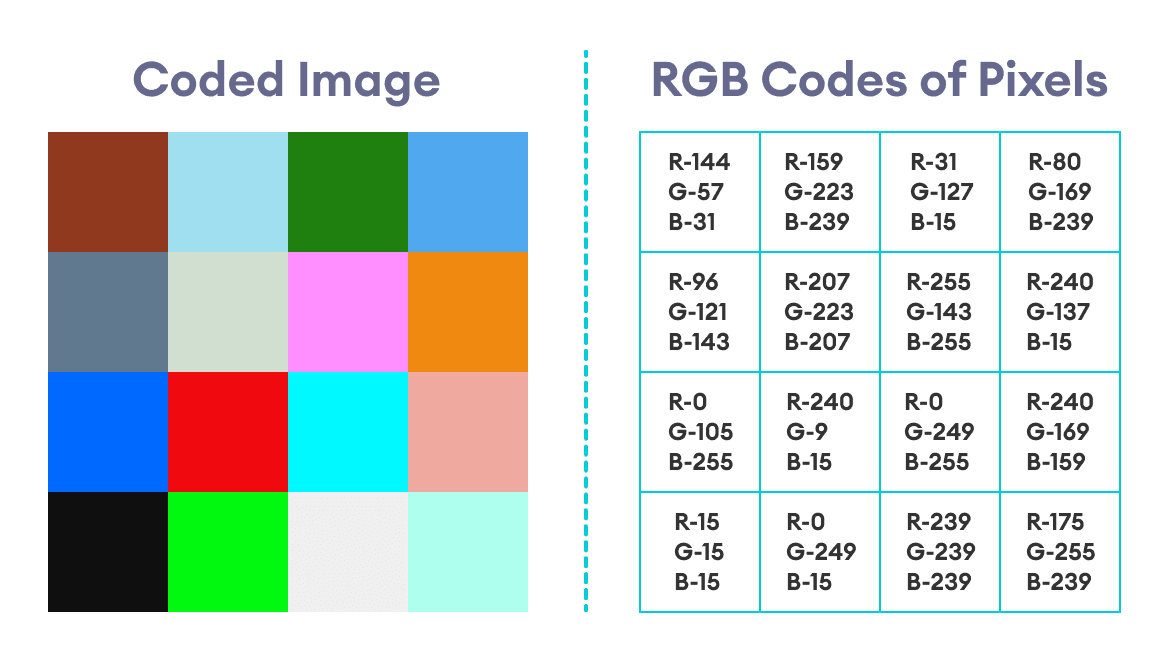
假设我们希望将下图隐藏在原始图像中。
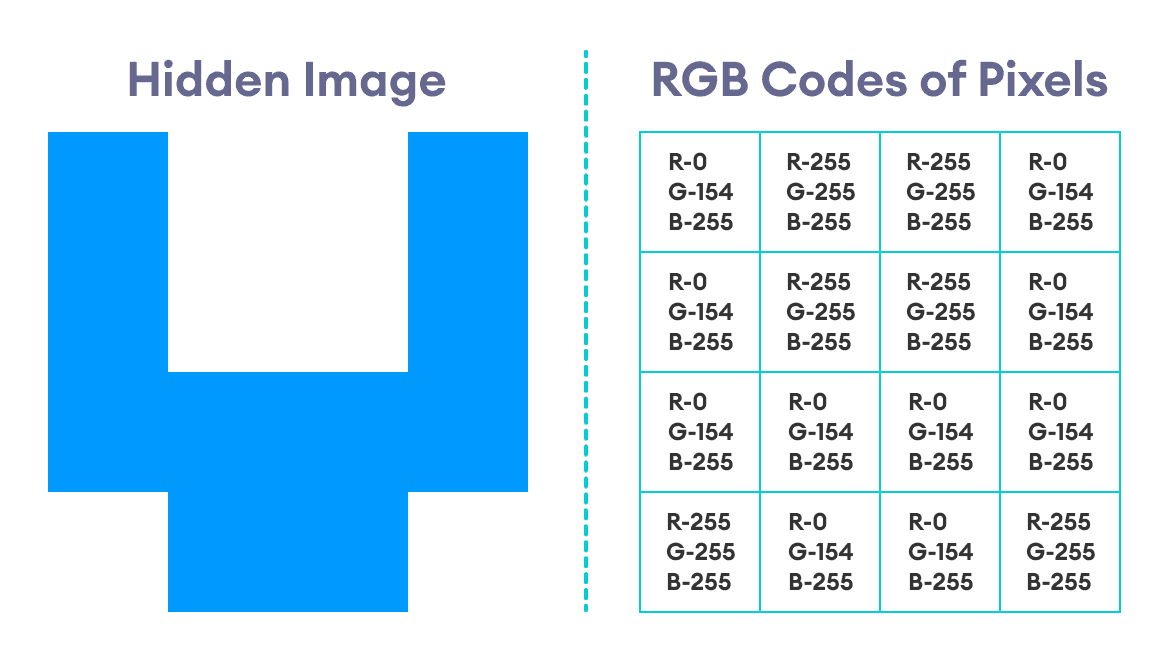
这张图像是一个简单的4x4图像,只包含两种颜色:蓝色和白色。蓝色的RGB代码是rgb(0, 154, 255)。
白色的代码当然是rgb(255, 255, 255)。
现在,让我们取原始图像的第一个像素和隐藏图像的第一个像素。
| 颜色 | 原始像素 | 隐藏像素 | 原始二进制 | 隐藏二进制 |
| 红色 | 144 | 0 | 1001 0000 | 0000 0000 |
| 绿色 | 56 | 154 | 0011 1000 | 1001 1010 |
| 蓝色 | 17 | 255 | 0001 0001 | 1111 1111 |
注意上表中已加粗的二进制代码部分:我们将原始像素二进制代码的最后四位替换为隐藏像素二进制代码的前四位。
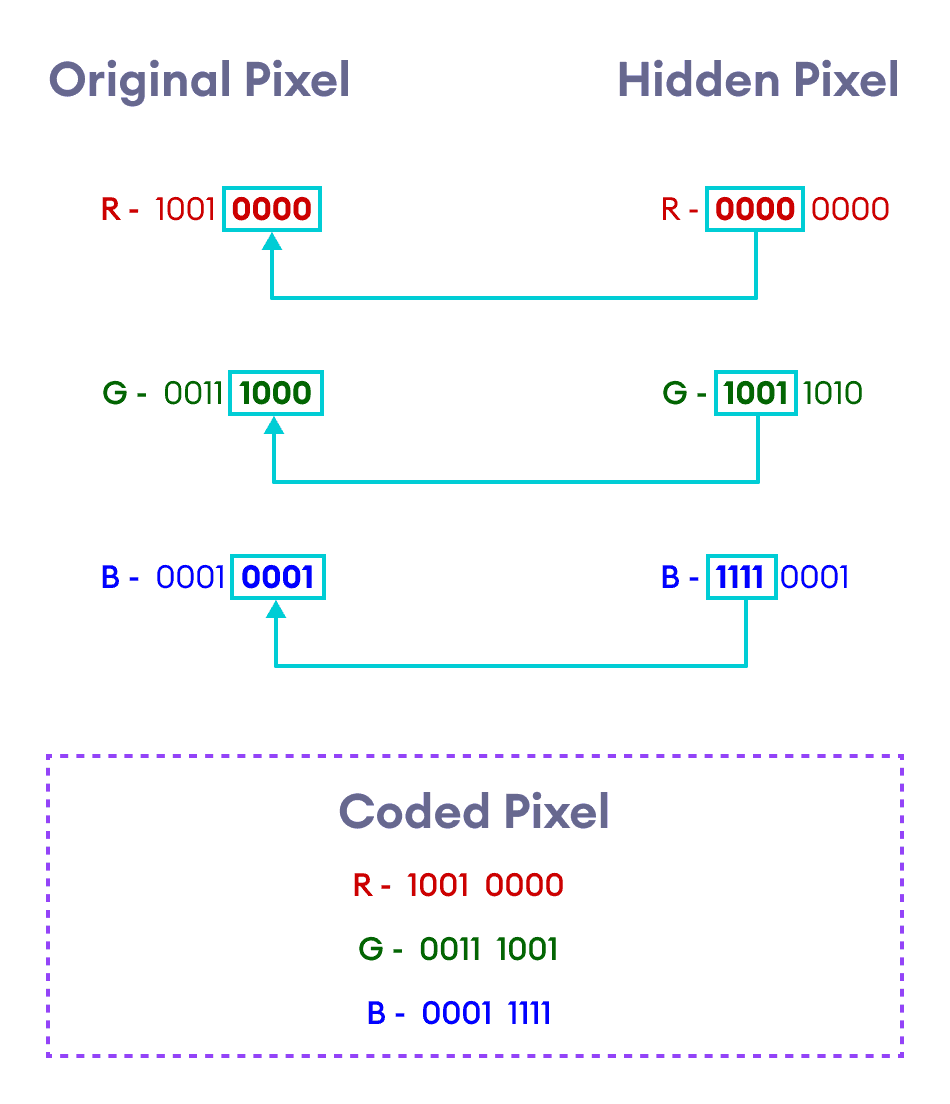
我们对剩余的像素重复相同的过程。生成的图像及其每个像素的RGB代码将是:
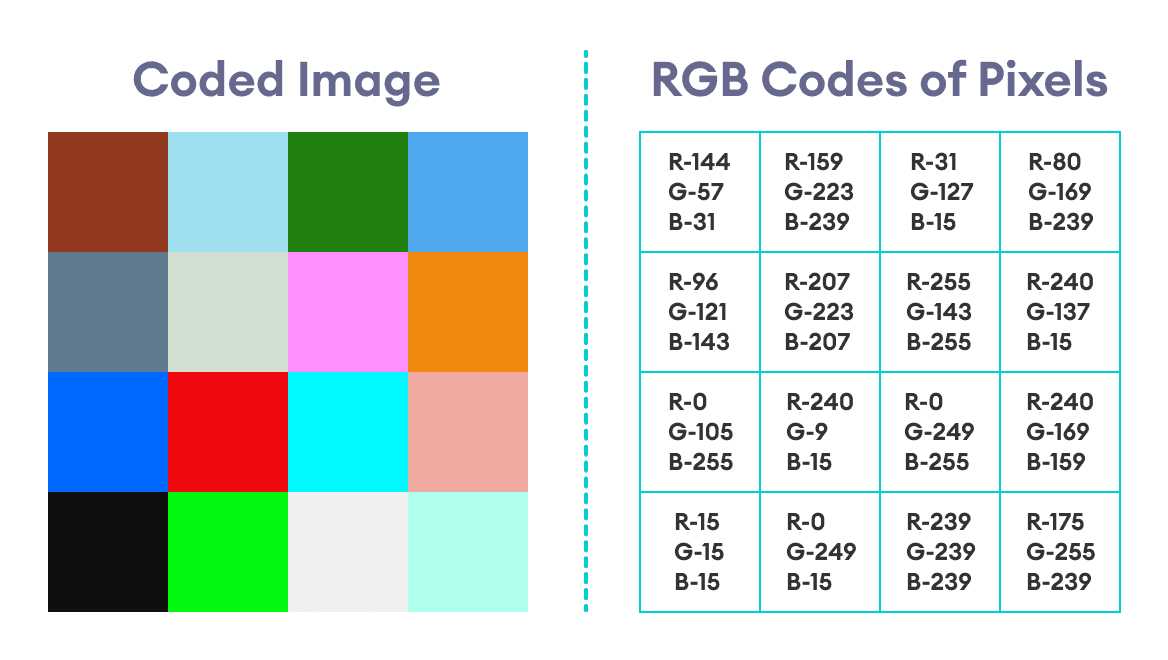
步骤3b:检索隐藏图像
我们现在通过反转步骤3a中概述的过程来检索隐藏图像。然而,正如我们很快就会看到的,这个过程并不完美,并且不能以与原始隐藏图像完全相同的像素信息检索隐藏图像。
图像检索步骤
- 找出每个像素的RGB代码并将其转换为二进制。
- 取每个红色、绿色和蓝色代码的最后四位,并在这些位右侧添加四个0。
- 这将得到隐藏图像相应像素的红色、绿色和蓝色代码。
- 对所有其他像素重复此过程以检索完整的隐藏图像。
这个过程由下图总结。
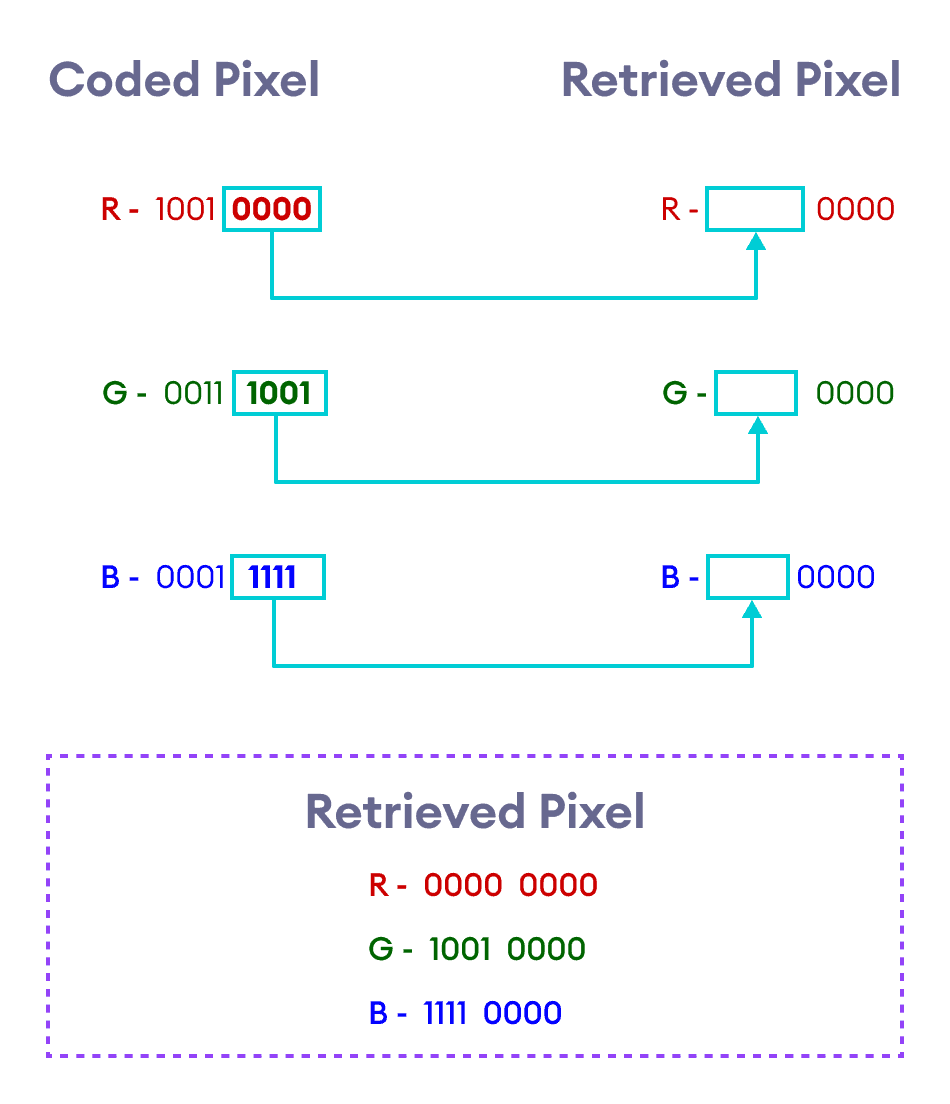
让我们取编码图像的前两个像素,并检索隐藏图像的相应像素。
检索第一个像素
| 颜色 | 编码像素 | 编码像素二进制 | 检索像素二进制 | 检索像素 |
| 红色 | 144 | 1001 0000 | 0000 0000 | 0 |
| 绿色 | 57 | 0011 1001 | 1001 0000 | 144 |
| 蓝色 | 31 | 0001 1111 | 1111 0000 | 240 |
因此,我们检索到的隐藏图像的第一个像素的RGB代码是rgb(0, 144, 240)。
请注意,我们检索到的RGB代码与我们最初创建隐藏图像时使用的RGB代码不同。原始隐藏图像第一个像素的RGB代码是rgb(0, 154, 255)。
然而,这两种颜色代码都产生非常相似的蓝色阴影。所以这个算法可能不完美,但它在很大程度上完成了任务。
检索第二个像素
| 颜色 | 编码像素 | 编码像素二进制 | 检索像素二进制 | 检索像素 |
| 红色 | 159 | 1001 1111 | 1111 0000 | 240 |
| 绿色 | 223 | 1101 1111 | 1111 0000 | 240 |
| 蓝色 | 239 | 1110 1111 | 1111 0000 | 240 |
因此,我们检索到的隐藏图像的第二个像素的RGB代码是rgb(240, 240, 240)。与第一个像素一样,这个像素也不是我们最初创建的隐藏图像RGB代码的精确匹配。检索到的像素是灰色的阴影,而原始像素是纯白色。
再一次,这表明这个过程并不完美,但它足以以与我们最初使用的图像非常相似的阴影检索隐藏图像。
最终检索到的隐藏图像——及其每个像素的RGB代码——如下所示。
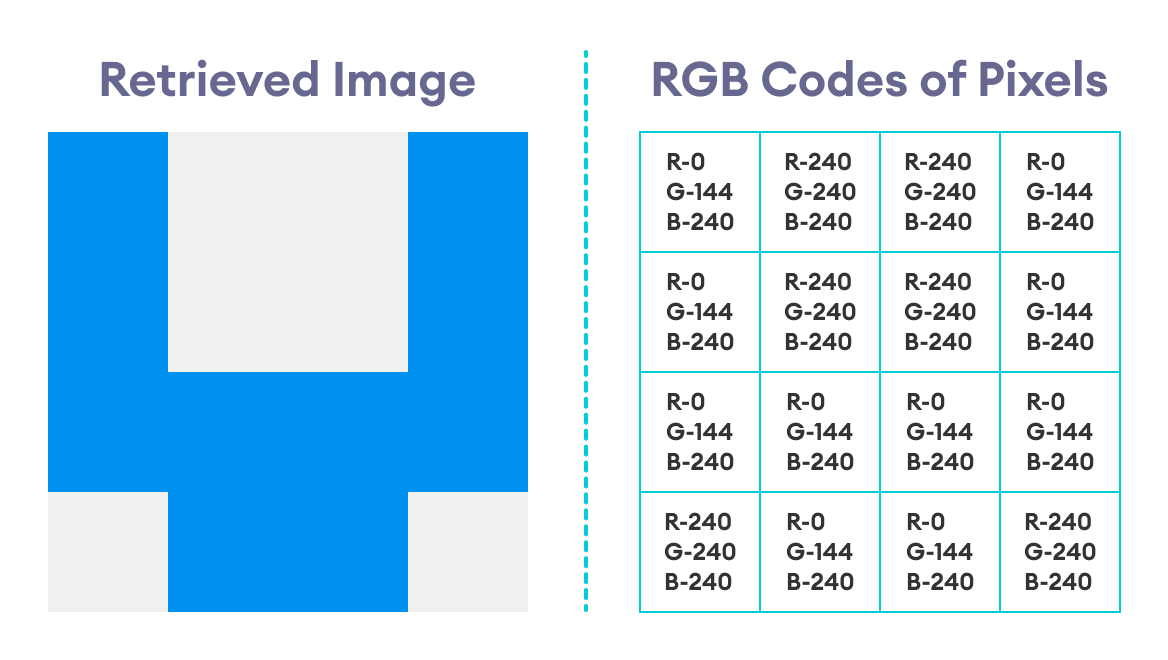
因此,我们终于提取了隐藏在另一张图像中的隐藏图像。
最后的思考和要点
- 像素是图像和图形在计算机和其他电子设备中显示的最小单位。
- 像素的颜色由编号代码确定,其中一些是RGB、HEX和HSL。
- 因此,隐写术需要对数系统有基本了解,例如二进制和十进制数系统(以及我们在这篇博文中没有讨论的十六进制数系统)。
- 在本文讨论的算法中,我们主要使用RGB代码,并将其转换为二进制以进行操作和隐藏消息。
- 在此算法中,仅操作RGB代码的最低有效位。
- 将一张图像隐藏在另一张图像中可能是一个不太完美的过程。
- 此处讨论的算法(和方法)特别取自伦敦大学金史密斯学院在Coursera上的一门名为“计算机科学数学”的在线课程。请访问该课程以获取更严谨和深入的内容。
订阅 Programiz 博客!
通过注册我们的电子邮件订阅,成为第一个接收 Programiz 的最新教程。还可以获得更多奖品,如最新的功能内部预览等等。


